之前在极客时间学习算法时做的笔记,截图很多引用自王争的《数据结构与算法之美》,推荐大家可以买书或者去极客时间学习。
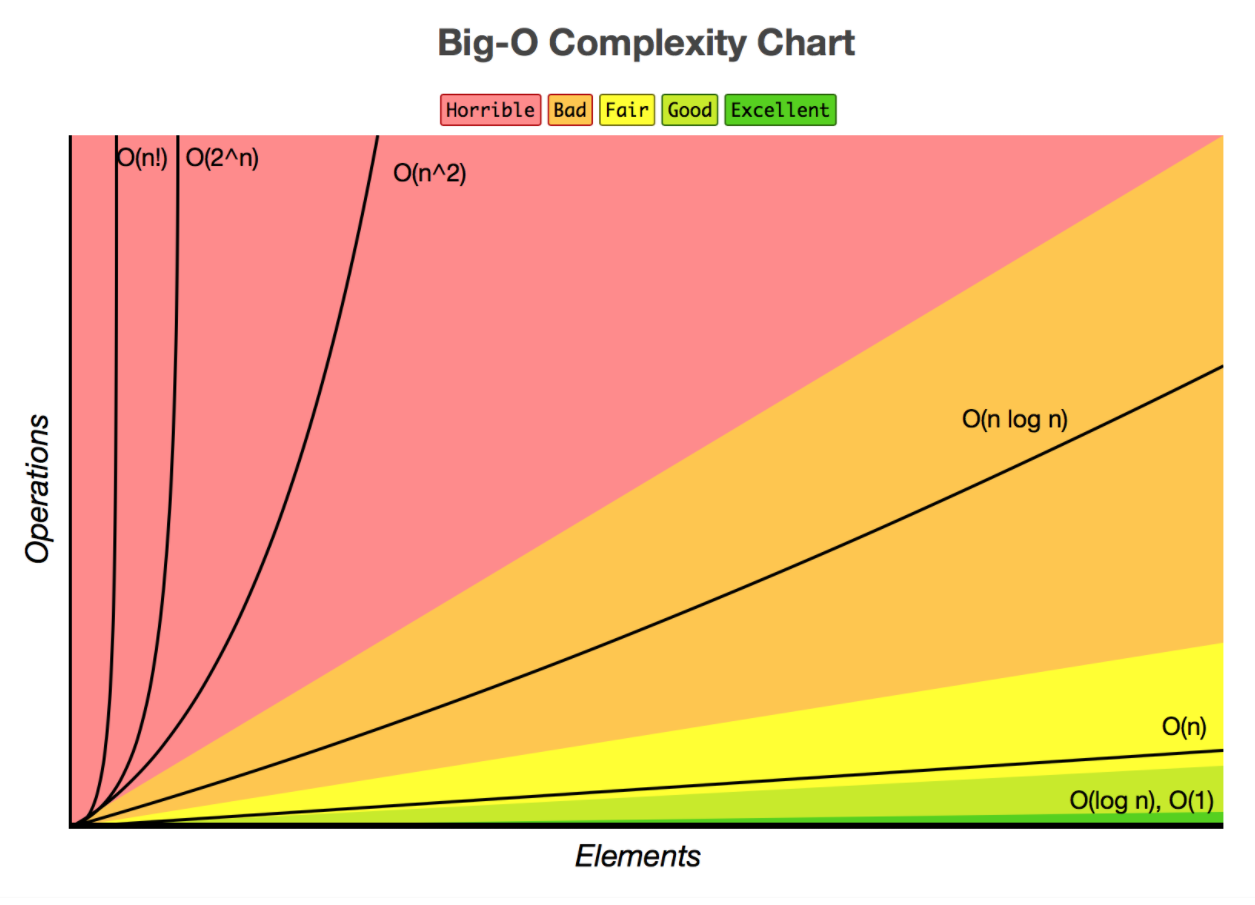
时间复杂度(O)
图
链表
写链表的注意事项
重点留意边界条件处理经常用来检查链表是否正确的边界4个边界条件:
- 如果链表为空时,代码是否能正常工作?
- 如果链表只包含一个节点时,代码是否能正常工作?
- 如果链表只包含两个节点时,代码是否能正常工作?
- 代码逻辑在处理头尾节点时是否能正常工作?
多练习,画图帮助思考
5个常见的链表操作:
- 单链表反转
- 链表中环的检测
- 两个有序链表合并
- 删除链表倒数第n个节点
- 求链表的中间节点
添加,打印
若用函数参数返回新产生的链表,则需要使用指向指针的指针! 下面的例子中的函数使用了可变长参数
#include <stdio.h>
#include <stdarg.h>
struct ListNode {
int value;
ListNode *next;
};
void PrintList(ListNode *p)
{
ListNode *t=p;
while(t)
{
printf("%d->", t->value);
t = t->next;
}
printf("NULL\n");
}
ListNode* AddToList(ListNode *p, int nArgs, ...)
{
va_list args;
int value;
ListNode* head = p;
va_start(args, nArgs);
if (nArgs <= 0)
return head;
for (int i=0; i<nArgs; i++)
{
value=va_arg(args, int);
ListNode *pNewNode = new ListNode;
pNewNode->value = value;
pNewNode->next = NULL;
if (p == NULL)
{
p = pNewNode;
head = pNewNode;
}
else
{
while(p->next)
p = p->next;
p->next = pNewNode;
}
}
va_end(args);
return head;
}
void AddValueToList(ListNode **p, int value)
{
ListNode *newp = new ListNode();
newp->value = value;
newp->next = NULL;
if (*p == NULL)
{
*p = newp;
}
else
{
ListNode *pt = *p;
while(pt->next != NULL)
pt = pt->next;
pt->next = newp;
}
return;
}
int main()
{
ListNode *pl = AddToList(NULL, 5, 1, 2, 3, 4, 5);
PrintList(pl);
ListNode *p;
AddValueToList(&p, 2);
AddValueToList(&p, 3);
AddValueToList(&p, 4);
PrintList(p);
return 0;
}
反转链表
三个变量,分别指向 前,中,后 需要考虑到程序到可靠性:输入NULL,单个节点,多个节点的ListNode
ListNode *reverseList(ListNode *head)
{
if (head == NULL)
return NULL;
ListNode *pre = head, *curr = head, *post = head->next;
pre->next = NULL;
while (post != NULL)
{
curr = post;
post = curr->next;
curr->next = pre;
pre = curr;
}
return curr;
}
递归方式:先走到链表底部,再一个个反转
ListNode* ReverseList2(ListNode *p)
{
if (p == NULL || p->next == NULL)
return p;
ListNode *pt = ReverseList2(p->next);
p->next->next = p;
p->next = NULL;
return pt;
}
网上的实现:使用递归和非递归两种方式
#include<iostream>
using namespace std;
struct node{
int val;
struct node* next;
node(int x) :val(x){}
};
/***非递归方式***/
node* reverseList(node* H)
{
if (H == NULL || H->next == NULL) //链表为空或者仅1个数直接返回
return H;
node* p = H, *newH = NULL;
while (p != NULL) //一直迭代到链尾
{
node* tmp = p->next; //暂存p下一个地址,防止变化指针指向后找不到后续的数
p->next = newH; //p->next指向前一个空间
newH = p; //新链表的头移动到p,扩长一步链表
p = tmp; //p指向原始链表p指向的下一个空间
}
return newH;
}
/***递归方式***/
node* In_reverseList(node* H)
{
if (H == NULL || H->next == NULL) //链表为空直接返回,而H->next为空是递归基
return H;
node* newHead = In_reverseList(H->next); //一直循环到链尾
H->next->next = H; //翻转链表的指向
H->next = NULL; //记得赋值NULL,防止链表错乱
return newHead; //新链表头永远指向的是原链表的链尾
}
int main()
{
node* first = new node(1);
node* second = new node(2);
node* third = new node(3);
node* forth = new node(4);
node* fifth = new node(5);
first->next = second;
second->next = third;
third->next = forth;
forth->next = fifth;
fifth->next = NULL;
//非递归实现
node* H1 = first;
H1 = reverseList(H1); //翻转
//递归实现
node* H2 = H1; //请在此设置断点查看H1变化,否则H2再翻转,H1已经发生变化
H2 = In_reverseList(H2); //再翻转
return 0;
}
从头到尾打印链表
FILO先入后出,则可以用栈,也可以用递归,递归本质上就是一个栈结构。
void PrintReverseList(ListNode *p)
{
if (p->next != NULL)
PrintReverseList(p->next);
printf("%d ", p->value);
}
删除链表节点
简单做法,遍历节点,那么时间复杂度就是O(n)。 优化做法,O(1),有可能O(1)。
void DeleteNode(ListNode **pp, ListNode *pToBeDeleted);
需要考虑:
- 删除最后一个节点
- 删除唯一的节点
- 节点不在list里面
- 特殊输入测试,比如NULL
void DeleteNode(ListNode **pp, ListNode *pToBeDeleted, bool bCheckNode = false)
{
if (*pp == pToBeDeleted)
{
if ((*pp)->next == NULL)
{
delete pToBeDeleted;
*pp = NULL;
}
else
{
*pp = (*pp)->next;
delete pToBeDeleted;
}
}
else if (bCheckNode || pToBeDeleted->next == NULL)
{
ListNode *p = *pp;
while(p->next != NULL)
{
if (p->next == pToBeDeleted)
{
p->next = pToBeDeleted->next;
delete pToBeDeleted;
break;
}
p = p->next;
}
}
else
{
pToBeDeleted->value = pToBeDeleted->next->value;
pToBeDeleted->next = pToBeDeleted->next->next;
}
}
从后往前找第N个节点(双指针)
使用两个指针
// n=1, means the last one.
ListNode* GetNodeFromEnd(ListNode *p, unsigned int n)
{
if (p == NULL || n == 0)
return NULL;
ListNode *p1 = p;
ListNode *p2 = p;
for (unsigned int i=1; i<n; i++)
{
p2 = p2->next;
if (p2 == NULL)
return p2;
}
while(p2->next != NULL)
{
p1 = p1->next;
p2 = p2->next;
}
return p1;
}
扩展问题:1. 找链表的中间节点,2. 判断是否形成了闭环 都可以使用双指针,一个每次走一步,一个每次走两步。
合并两个有序链表
用两个指针,一个指向头,一个在两个链表一步步比较下去
// p1, p2 is asc order.
ListNode *MergeList(ListNode *p1, ListNode *p2)
{
ListNode *ph = NULL; // 指向头
ListNode *pf = NULL; // 串联使用的变量
while(p1 != NULL || p2 != NULL)
{
if (p1 != NULL && p2 != NULL)
{
if (p1->value > p2->value)
{
if (ph == NULL)
{
ph = p2;
}
else
{
pf->next = p2;
}
pf = p2;
p2 = p2->next;
}
else
{
if (ph == NULL)
{
ph = p1;
}
else
{
pf->next = p1;
}
pf = p1;
p1 = p1->next;
}
}
else if (p1 == NULL)
{
if (ph == NULL)
return p2;
else
{
pf->next = p2;
return ph;
}
}
else if (p2 == NULL)
{
if (ph == NULL)
return p1;
else
{
pf->next = p1;
return ph;
}
}
}
return ph;
}
使用递归
ListNode *MergeList2(ListNode *p1, ListNode *p2)
{
if (p1 == NULL)
return p2;
if (p2 == NULL)
return p1;
ListNode *pr = NULL;
if (p1->value < p2->value)
{
pr = p1;
pr->next = MergeList2(p1->next, p2);
}
else
{
pr = p2;
pr->next = MergeList2(p1, p2->next);
}
return pr;
}
找两个链表中的第一个公共节点
单向链表,那么有公共节点的话,后面每一个节点都相同。两个链表只能是Y型。找到长度,一个先走。
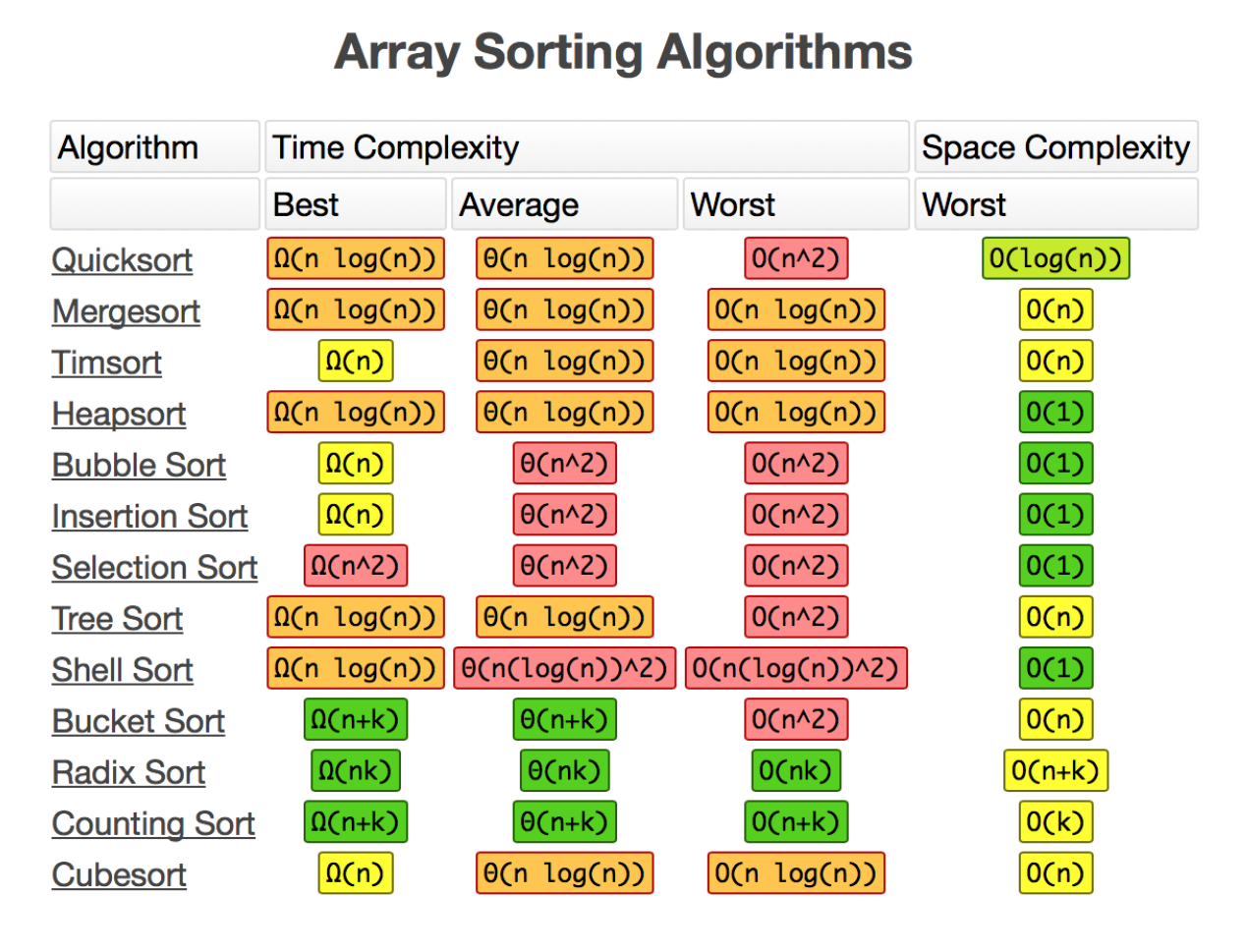
排序
评价一个排序算法,需要考虑:执行效率,内存消耗,稳定性。

- 稳定性是说排序后相同的元素,在排序后的顺序不发生变化。
- 原地排序是说不需要分配多余的内存,某些情况可能很重要。
O(n^2)
冒泡 bubble sort
从前往后,每次比较两数,把最小或者最大的数交换到后面去。 改进:有可能提前排好。如果没有交换发生,就说明已排好了。 时间复杂度是O(n^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 冒泡排序,a表示数组,n表示数组大小
public void bubbleSort(int[] a, int n) {
if (n <= 1) return;
for (int i = 0; i < n; ++i) {
// 提前退出冒泡循环的标志位
boolean flag = false;
for (int j = 0; j < n - i - 1; ++j) {
if (a[j] > a[j+1]) { // 交换
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
flag = true; // 表示有数据交换
}
}
if (!flag) break; // 没有数据交换,提前退出
}
}

插入排序 Insertion sort
动态地往有序集合中添加数据,通过这种方式保持集合中的数据一直有序。 时间复杂度是O(n^2),但速度比冒泡快,因为冒泡排序要中数据交换的次数更多。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 插入排序,a表示数组,n表示数组大小
public void insertionSort(int[] a, int n) {
if (n <= 1) return;
for (int i = 1; i < n; ++i) {
int value = a[i];
int j = i - 1;
// 查找插入的位置
for (; j >= 0; --j) {
if (a[j] > value) {
a[j+1] = a[j]; // 数据移动
} else {
break;
}
}
a[j+1] = value; // 插入数据(注意此时是j+1)
}
}

选择排序 Selection Sort
类似插入排序,但是选择排序每次会从未排序区间找到最小的元素,将其放到已排序区间的末尾。
O(nlogn)
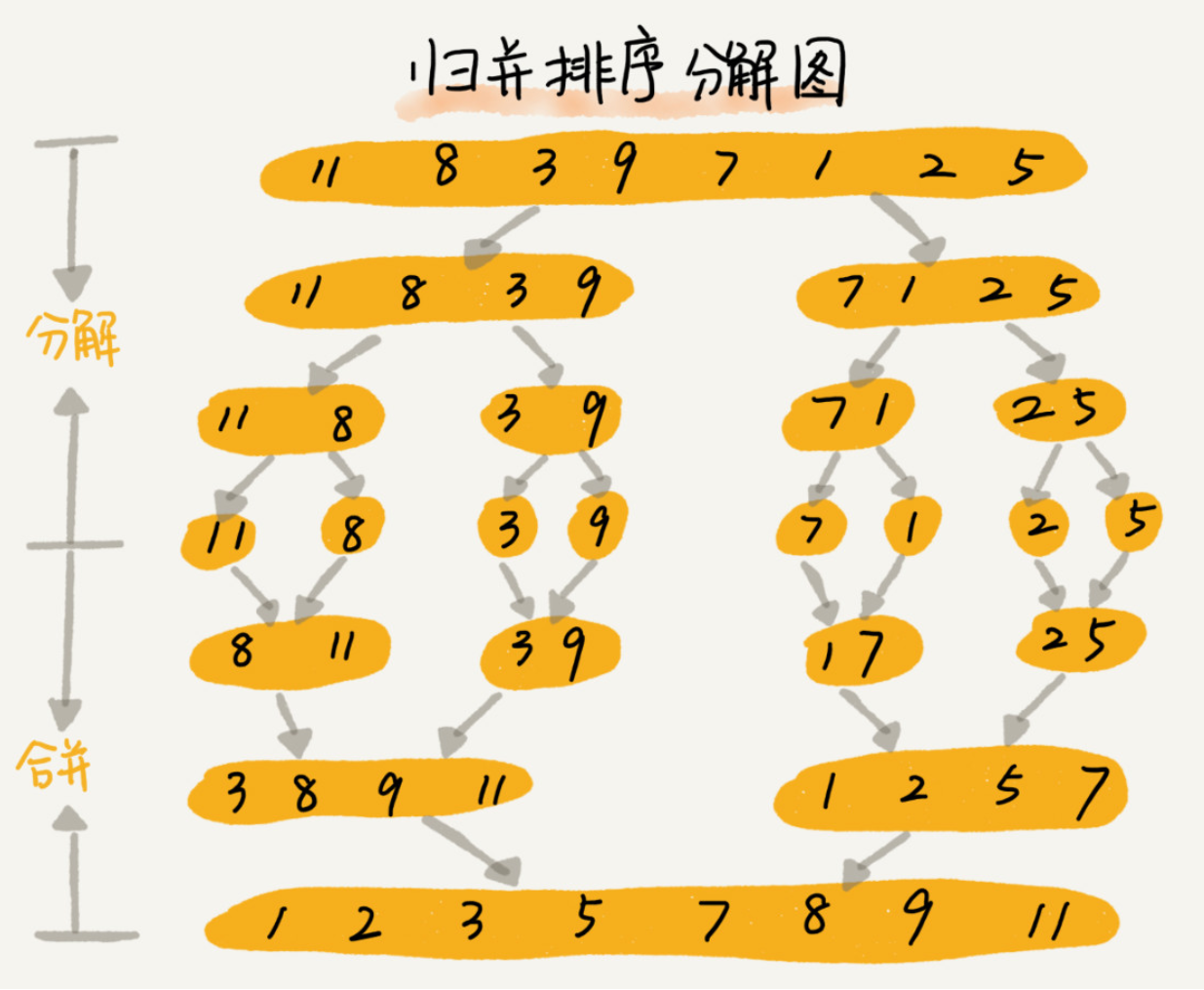
归并排序 Merge Sort
先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排序好的两部分合并在一起,这样整个数组就都有序了。 归并使用的是分治思想,将一个大问题分解成小问题来解决,小问题解决了,大问题也就解决了。
1
2
3
4
5
递推公式:
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
终止条件:
p >= r 不用再继续分解
快速排序 Quick Sort
和递归排序一样,也是分治的思想。 在要排序的数组下标从p到r之间,选任意一个数据作为pivot分区点。遍历p到r,将小于pivot的放左边,大于的放右边。
1
2
3
4
5
递推公式:
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1… r)
终止条件:
p >= r
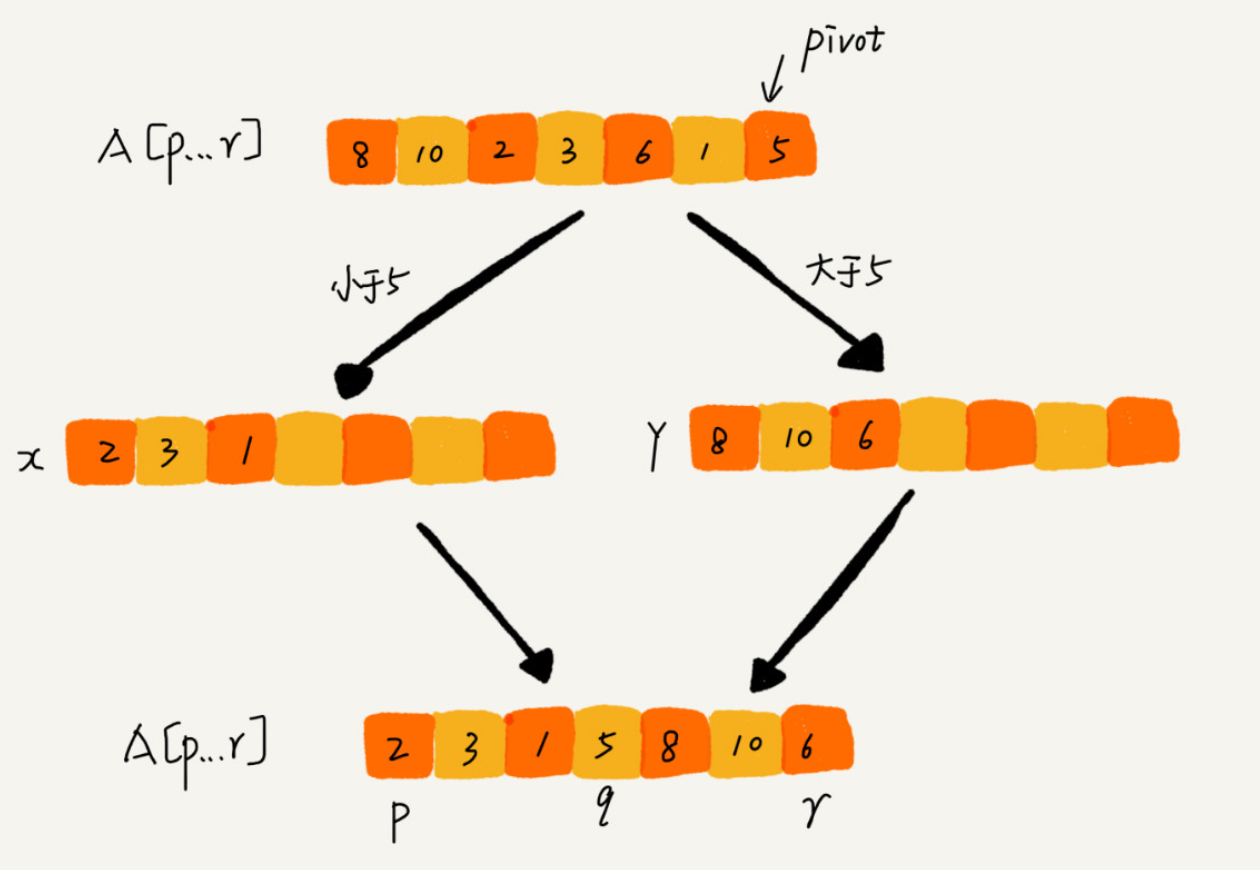
上面的思路需要额外的内存空间,所以不是原地排序算法了。下面的伪代码实现了原地排序
1
2
3
4
5
6
7
8
9
10
11
12
13
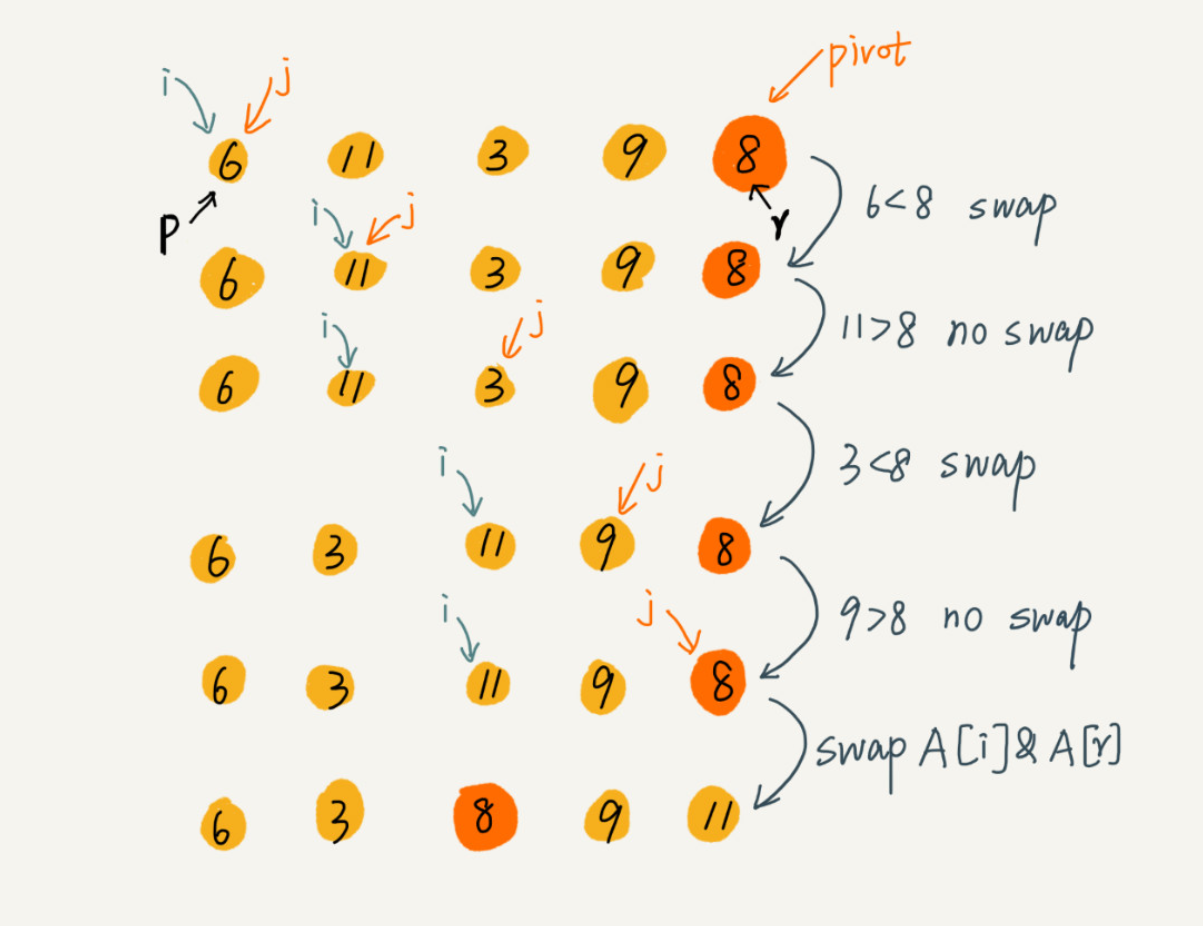
// 使用游标 i 将A[p...r-1]分成两部分,A[p...i-1]的元素都是小于pivot的,当作已处理区,A[i...r-1]是未处理区。每次都从A[i...r-1]中取出一个元素A[j],与pivot比较,小于pivot的,将其加入已处理区的尾部,也就是A[i]的位置。
partition(A, p, r) {
pivot := A[r]
i := p
for j := p to r-1 do {
if A[j] < pivot {
swap A[i] with A[j]
i := i+1
}
}
swap A[i] with A[r]
return i
}
如何优化快速排序:最理想的分区点是被分开的两个分区中,数据的数量差不多。
- 三数取中,或者多个数取中,做为分区点。
- 随机取一个元素做分区点。
堆
堆的基本信息(完全二叉树,插入删除都是O(logn))
堆是一种特殊的树。满足下面两点,就是堆: 第一点,堆必须是一个完全二叉树。完全二叉树要求,除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列。 第二点,堆中的每个节点的值必须大于等于(或者小于等于)其子树中每个节点的值。
注意,并不要求上层的节点比下层任一节点大,只要求比自己的子节点大。
对于每个节点的值都大于等于子树中每个节点值的堆,我们叫作“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆,我们叫作“小顶堆”。
完全二叉树适合用数组来存储。数组中下标为 i 的节点的左子节点,就是下标为 i∗2 的节点,右子节点就是下标为 i∗2+1 的节点,父节点就是下标为 i/2 的节点。
往堆中插入数据
可以先把新插入的数据放最后,让新插入的节点与父节点对比大小。如果不满足子节点小于等于父节点的大小关系,我们就互换两个节点。一直重复这个过程,直到父子节点之间满足刚说的那种大小关系。
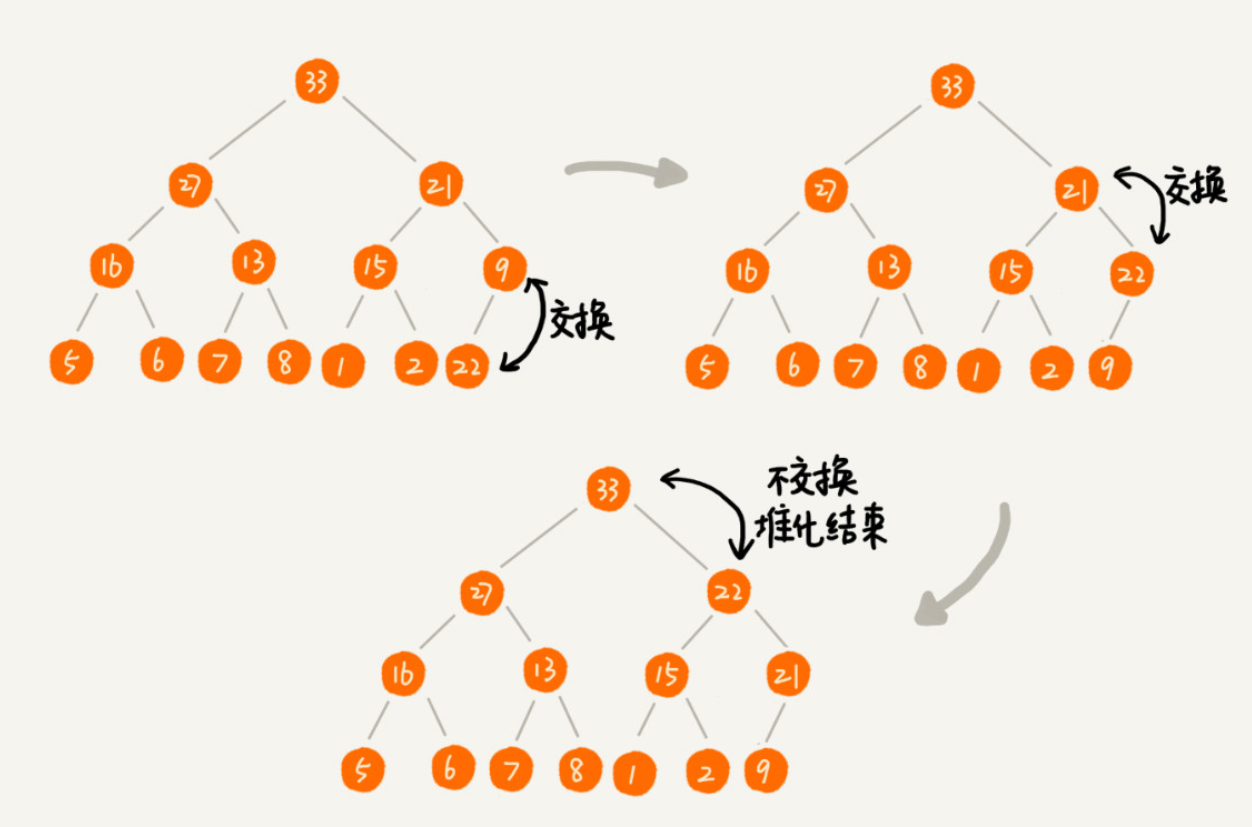
从堆中删除数据
我们把最后一个节点放到要删除的数据位置,然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的,互换两个节点,并且重复进行这个过程,直到父子节点之间满足大小关系为止。这就是从上往下的堆化方法。因为我们移除的是数组中的最后一个元素,而在堆化的过程中,都是交换操作,不会出现数组中的“空洞”,所以这种方法堆化之后的结果,肯定满足完全二叉树的特性。
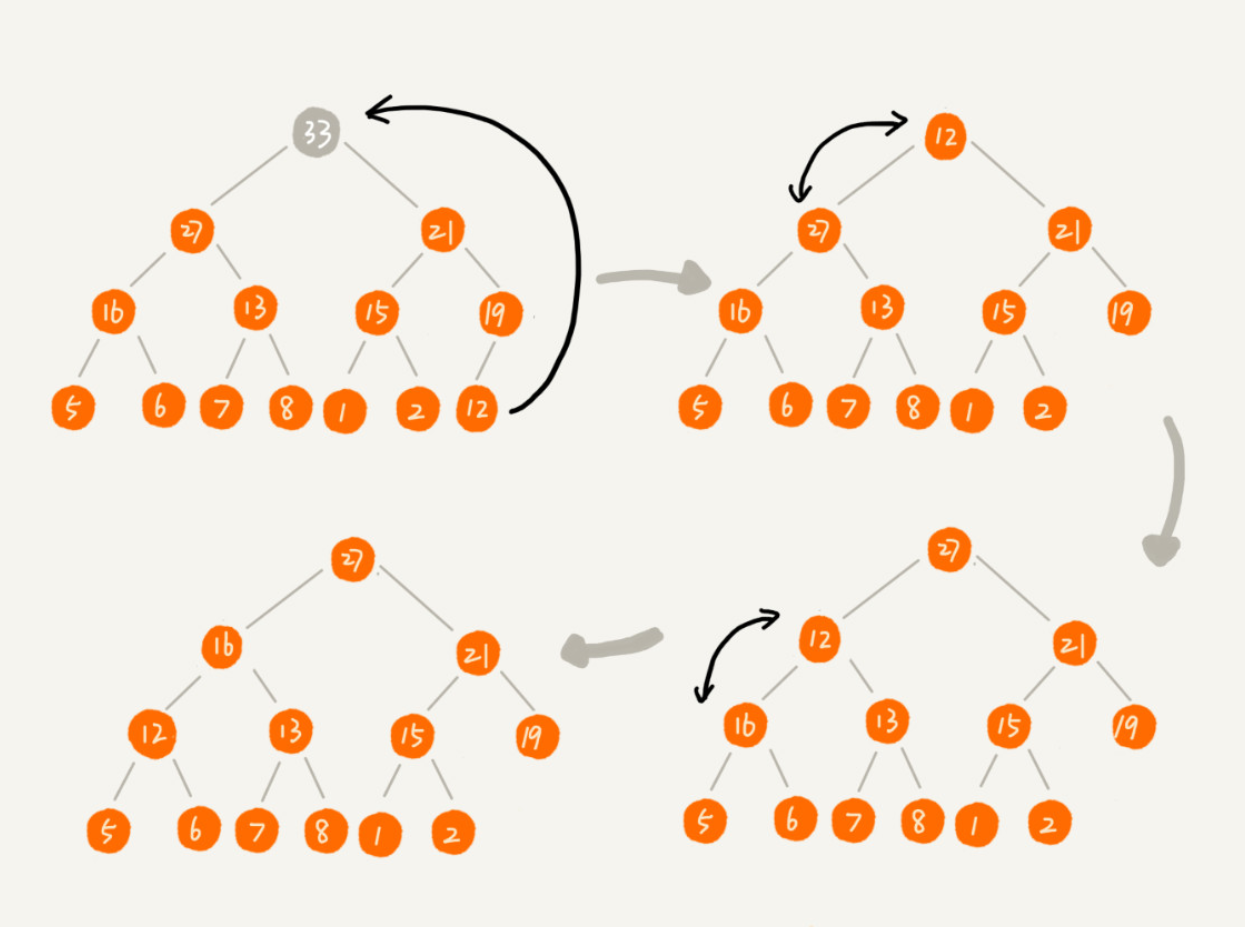
在堆中插入和删除数据的时间复杂度都是O(logn)。
堆排序O(原地排序,nlogn)
我们将下标从 n/2 到 1 的节点,依次进行从上到下的堆化操作,然后就可以将数组中的数据组织成堆这种数据结构。接下来,我们迭代地将堆顶的元素放到堆的末尾,并将堆的大小减一,然后再堆化,重复这个过程,直到堆中只剩下一个元素,整个数组中的数据就都有序排列了。
整个堆排序的过程,都只需要极个别临时存储空间,所以堆排序是原地排序算法。堆排序包括建堆和排序两个操作,建堆过程的时间复杂度是 O(n),排序过程的时间复杂度是 O(nlogn),所以,堆排序整体的时间复杂度是 O(nlogn)。
在实际开发中,为什么快速排序要比堆排序性能好?
- 堆排序数据访问的方式没有快速排序友好。跳着访问,对 CPU 缓存是不友好的。
- 对于同样的数据,在排序过程中,堆排序算法的数据交换次数要多于快速排序。
堆的应用
- 优先级队列 a. 合并多个有序文件(各个文件都取出第一个,然后比较,再在相关的文件取下一个,比较的时候就可以用堆,插入、删除都是O(logn)) b. 高性能定时器(多个定时任务需要执行,构造一个小顶堆,堆顶是最近需要执行的。)
- 求 Top K 可以维护一个大小为 K 的 小顶堆,顺序遍历数组,从数组中取出数据与堆顶元素比较。如果比堆顶元素大,我们就把堆顶元素删除,并且将这个元素插入到堆中;如果比堆顶元素小,则不做处理,继续遍历数组。这样等数组中的数据都遍历完之后,堆中的数据就是前 K 大数据了。
- 求 中位数或某一百分位的数 如果我们面对的是动态数据集合,中位数在不停地变动,如果再用先排序的方法,每次询问中位数的时候,都要先进行排序,那效率就不高了。 如要求排在80%位的数据。那么就维护两个堆,假设当前总数据的个数是 n,大顶堆中保存 n乘80% 个数据,小顶堆中保存 n乘20% 个数据。大顶堆堆顶的数据就是我们要找的 80%的数据。每次插入一个数据的时候,我们要判断这个数据跟大顶堆和小顶堆堆顶数据的大小关系,然后决定插入到哪个堆中。如果这个新插入的数据比大顶堆的堆顶数据小,那就插入大顶堆;如果这个新插入的数据比小顶堆的堆顶数据大,那就插入小顶堆。同时需维护两个堆中20:80的比例,可能需要将一个堆中的数据移动到另外一个中。 通过这样的方法,每次插入数据,可能会涉及几个数据的堆化操作,所以时间复杂度是 O(logn)。但取值时直接返回大顶堆中的堆顶数据即可,时间复杂度是 O(1)。
堆的相关代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
public class Heap {
private int[] a; // 数组,从下标1开始存储数据
private int n; // 堆可以存储的最大数据个数
private int count; // 堆中已经存储的数据个数
public Heap(int capacity) {
a = new int[capacity + 1];
n = capacity;
count = 0;
}
public void insert(int data) {
if (count >= n) return; // 堆满了
++count;
a[count] = data;
int i = count;
while (i/2 > 0 && a[i] > a[i/2]) { // 自下往上堆化
swap(a, i, i/2); // swap()函数作用:交换下标为i和i/2的两个元素
i = i/2;
}
}
private static void buildHeap(int[] a, int n) {
for (int i = n/2; i >= 1; --i) {
heapify(a, n, i);
}
}
public void removeMax() {
if (count == 0) return -1; // 堆中没有数据
a[1] = a[count];
--count;
heapify(a, count, 1);
}
private void heapify(int[] a, int n, int i) { // 自上往下堆化
while (true) {
int maxPos = i;
if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
if (maxPos == i) break;
swap(a, i, maxPos);
i = maxPos;
}
}
// n表示数据的个数,数组a中的数据从下标1到n的位置。
public static void sort(int[] a, int n) {
buildHeap(a, n);
int k = n;
while (k > 1) {
swap(a, 1, k);
--k;
heapify(a, k, 1);
}
}
}
buildHeap() 进行堆化的时候,我们对下标从 n/2 开始到 1 的数据进行堆化,下标是 n/2+1 到 n 的节点是叶子节点,我们不需要堆化。实际上,对于完全二叉树来说,下标从 n/2+1 到 n 的节点都是叶子节点。
O(n)
桶排序 Bucket Sort
如果要排序的数据有n个,把它们划分到m个有序的桶内,每个桶内的数据再单独进行排序。排完序后,按顺序把每个桶里的数据依次取出,组成的序列就是有序的了。 当m接近n时,时间复杂度接近O(n)。极端情况下,数据被划分到一个桶中,就退化为O(nlogn)。 如果某个区间划分的数据太多,可以在这个区间内,再次使用桶排序来划分处理。 桶排序比较适合用在外部排序中,比如数据保存在外部磁盘中,数据量比较大,内存有限,无法将数据全部加载到内存中。

计数排序 Counting Sort
可以看作是桶排序的一种特殊情况。
假设8个考生,分数在0到5之间。这 8 个考生的成绩我们放在一个数组 A[8] 中,它们分别是:2,5,3,0,2,3,0,3。若按成绩排序,使用大小是6的数组C[6]表示桶,其中下标对应分数。不过C[6]内保存的不是考生,而是对应分数的考生个数。只需要遍历一次考生分数,就可以得到C[6]。 假设上面3分的考生有3个,小于3分的考生有4个,那么成绩为3分的考生再排序后的数组R[8]中,会保存在下标4、5、6的位置。
下面的方法快速计算出最终排序后的数组: 我们对 C[6] 数组顺序求和,C[6] 存储的数据就变成了下面这样子。C[k] 里存储小于等于分数 k 的考生个数。
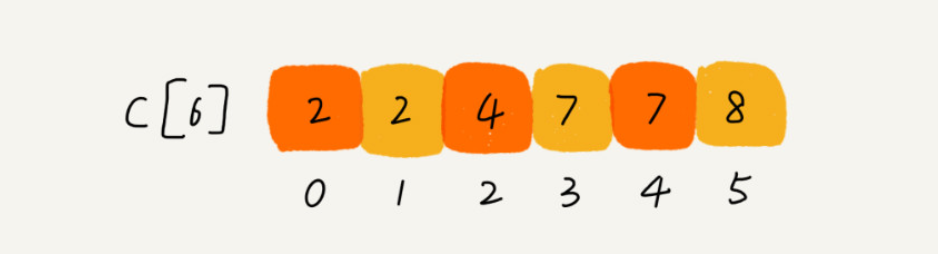
我们从后到前依次扫描数组 A。比如,当扫描到 3 时,我们可以从数组 C 中取出下标为 3 的值 7,也就是说,到目前为止,包括自己在内,分数小于等于 3 的考生有 7 个,也就是说 3 是数组 R 中的第 7 个元素(也就是数组 R 中下标为 6 的位置)。当 3 放入到数组 R 中后,小于等于 3 的元素就只剩下了 6 个了,所以相应的 C[3] 要减 1,变成 6。

计数排序只能用在数据范围不大的场景中,如果数据范围 k 比要排序的数据 n 大很多,就不适合用计数排序了。而且,计数排序只能给非负整数排序,如果要排序的数据是其他类型的,要将其在不改变相对大小的情况下,转化为非负整数。
基数排序 Radix Sort
如果我们排序10w个手机号码,或者排序字典中的所有单词,可以用快排,时间复杂度到O(nlogn)。但不能用桶排序或者计数排序,因为手机号码11位,范围太大。针对这类排序,可以使用基数排序,时间复杂度位O(n)。
原理:可以从先排序最后一位,再依次排序前一位。注意这个每一位的排序算法要是稳定的。每一位的排序可以用桶排序或者计数排序。 排序英文单词时,由于长度不同,可以把所有的单词都补齐到相同长度,位数不够的可以在后门补”0”。
图
图的基本概念:无向图、有向图、带权图、顶点、边、度、入度、出度。 场景: 微博:有向图,可以单方向关注。 微信:无向图,只能双向关注。 QQ的好友亲密度:带权图。
存储
邻接矩阵 Adjacency Matrix
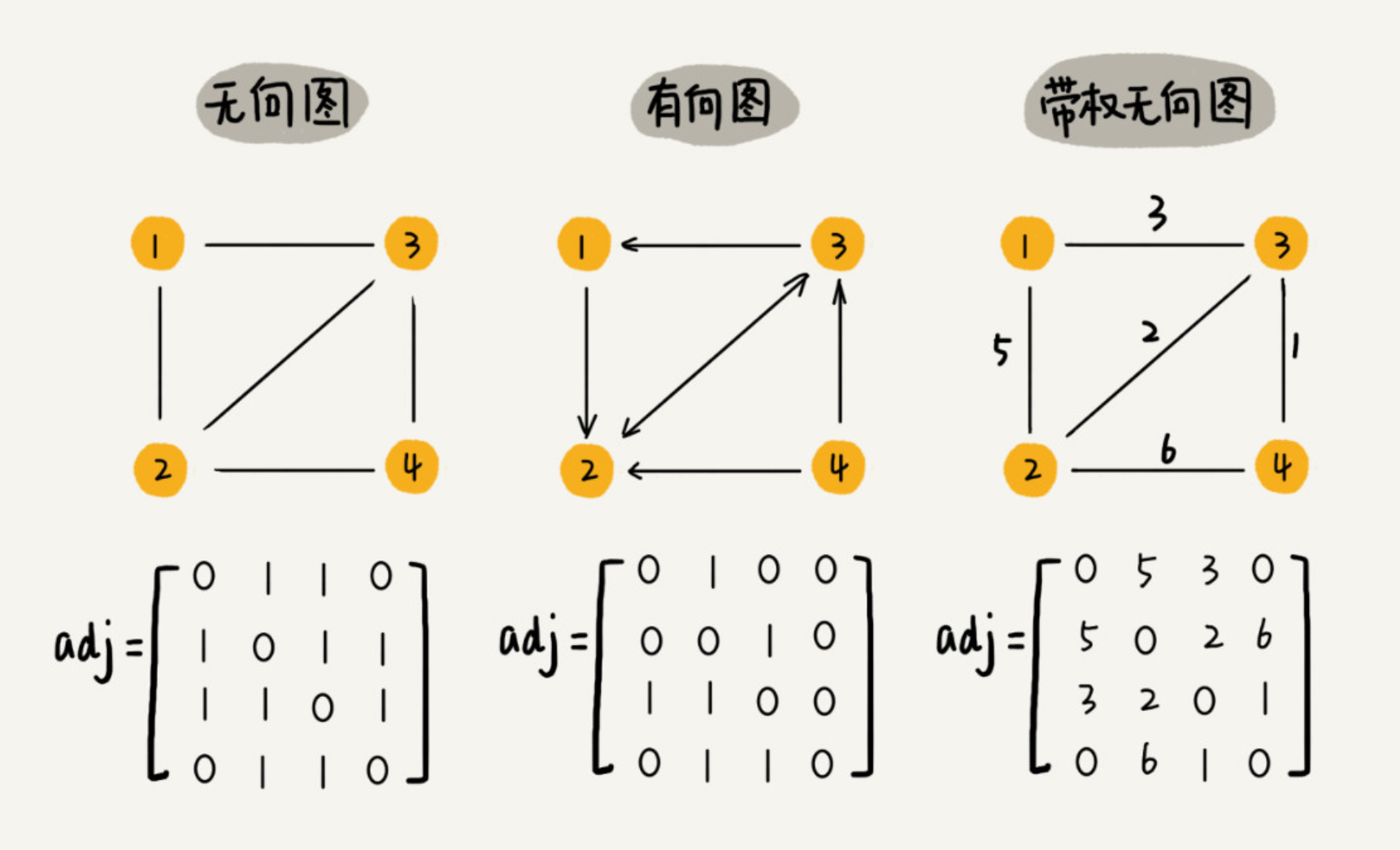
邻接矩阵的底层依赖一个二维数组。对于无向图来说,如果顶点 i 与顶点 j 之间有边,我们就将 A[i][j] 和 A[j][i] 标记为 1;对于有向图来说,如果顶点 i 到顶点 j 之间,有一条箭头从顶点 i 指向顶点 j 的边,那我们就将 A[i][j] 标记为 1。同理,如果有一条箭头从顶点 j 指向顶点 i 的边,我们就将 A[j][i] 标记为 1。对于带权图,数组中就存储相应的权重。
邻接矩阵存储方法的缺点是比较浪费空间,但是优点是查询效率高,而且方便矩阵运算。
邻接表 Adjacency List
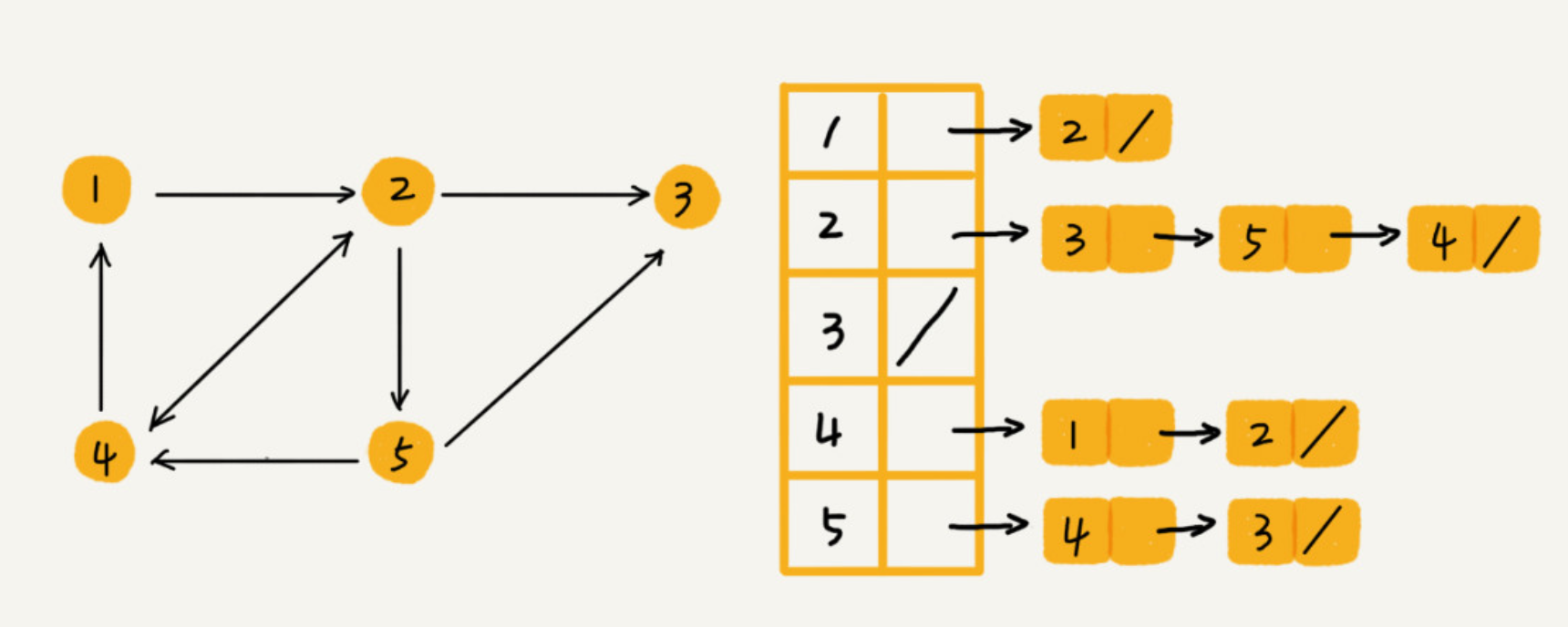
邻接表存储方法中每个顶点都对应一个链表,存储与其相连接的其他顶点。尽管邻接表的存储方式比较节省存储空间,但链表不方便查找,所以查询效率没有邻接矩阵存储方式高。针对这个问题,邻接表还有改进升级版,即将链表换成更加高效的动态数据结构,比如平衡二叉查找树、跳表、散列表等。
邻接表的搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Graph { // 无向图
private int v; // 顶点的个数
private LinkedList<Integer> adj[]; // 邻接表
public Graph(int v) {
this.v = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i) {
adj[i] = new LinkedList<>();
}
}
public void addEdge(int s, int t) { // 无向图一条边存两次
adj[s].add(t);
adj[t].add(s);
}
}
广度优先搜索 Breadth-First-Search
借助一个队列! 三个重要的辅助变量visited, queue, prev:
- visited 是用来记录已经被访问的顶点,用来避免顶点被重复访问。如果顶点 q 被访问,那相应的 visited[q] 会被设置为 true。
- queue 是一个队列,用来存储已经被访问、但相连的顶点还没有被访问的顶点。
- prev 用来记录搜索路径。这个路径是反向存储的。prev[w] 存储的是,顶点 w 是从哪个前驱顶点遍历过来的。比如,我们通过顶点 2 的邻接表访问到顶点 3,那 prev[3] 就等于 2。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public void bfs(int s, int t) {
if (s == t) return;
boolean[] visited = new boolean[v];
visited[s]=true;
Queue<Integer> queue = new LinkedList<>();
queue.add(s);
int[] prev = new int[v];
for (int i = 0; i < v; ++i) {
prev[i] = -1;
}
while (queue.size() != 0) {
int w = queue.poll();
for (int i = 0; i < adj[w].size(); ++i) {
int q = adj[w].get(i);
if (!visited[q]) {
prev[q] = w;
if (q == t) {
print(prev, s, t);
return;
}
visited[q] = true;
queue.add(q);
}
}
}
}
private void print(int[] prev, int s, int t) { // 递归打印s->t的路径
if (prev[t] != -1 && t != s) {
print(prev, s, prev[t]);
}
System.out.print(t + " ");
}
深度优先搜索 Depth-First-Search
借助一个栈! 深度优先搜索用的是一种比较著名的算法思想,回溯思想。这种思想解决问题的过程,非常适合用递归来实现。 也需要用到 visited, prev 变量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
boolean found = false; // 全局变量或者类成员变量
public void dfs(int s, int t) {
found = false;
boolean[] visited = new boolean[v];
int[] prev = new int[v];
for (int i = 0; i < v; ++i) {
prev[i] = -1;
}
recurDfs(s, t, visited, prev);
print(prev, s, t);
}
private void recurDfs(int w, int t, boolean[] visited, int[] prev) {
if (found == true) return;
visited[w] = true;
if (w == t) {
found = true;
return;
}
for (int i = 0; i < adj[w].size(); ++i) {
int q = adj[w].get(i);
if (!visited[q]) {
prev[q] = w;
recurDfs(q, t, visited, prev);
}
}
}
字符串匹配
BF算法 Brute Force
概念:主串,模式串。比方说,我们在字符串 A 中查找字符串 B,那字符串 A 就是主串,字符串 B 就是模式串。我们把主串的长度记作 n,模式串的长度记作 m。
BF 算法的思想可以用一句话来概括,那就是,我们在主串中,检查起始位置分别是 0、1、2…n-m 且长度为 m 的 n-m+1 个子串,看有没有跟模式串匹配的。
尽管理论上,BF 算法的时间复杂度很高,是 O(n*m),但在实际的开发中,它却是一个比较常用的字符串匹配算法。
RK算法 Rabin-Karp
BF算法的优化: 将子串和模式串的字符串比较,转换成了哈希值的比较。这里的哈希值是将字符串转换成数字。比如字符串只出现a-z 26个字母,那么bca可以转换为1x26x26+2x26+0x26。26的阶乘可以提前计算出来提高速度。
BM算法 Boyer-Moore
BM 算法包含两部分,分别是坏字符规则(bad character rule)和好后缀规则(good suffix shift)。
坏字符规则,匹配字符串的时候从右往左匹配。发现不一致字符时,再看不一致字符在不在模式串中,如果不在,直接将模式串移动到主串的该字符后。
好后缀的处理规则中最核心的内容:在模式串中,查找跟好后缀匹配的另一个子串;在好后缀的后缀子串中,查找最长的、能跟模式串前缀子串匹配的后缀子串。
KMP算法
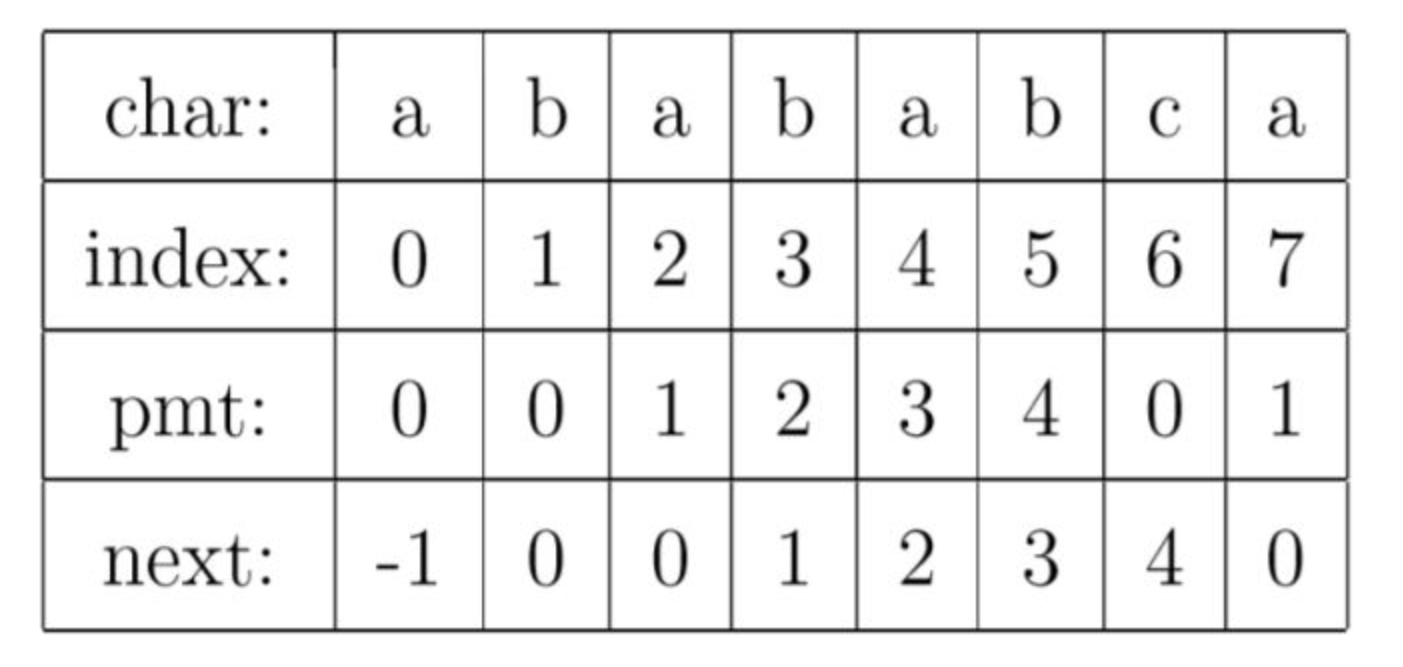
KMP 算法对 BF 算法进行改进,引入了 next 数组,让匹配失败时,尽可能将模式串往后多滑动几位。
重点是理解PMT数组:PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。
时间复杂度是O(m+n),空间复杂度是O(m)。
Trie树
场景:搜索引擎的搜索关键词提示。 Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。
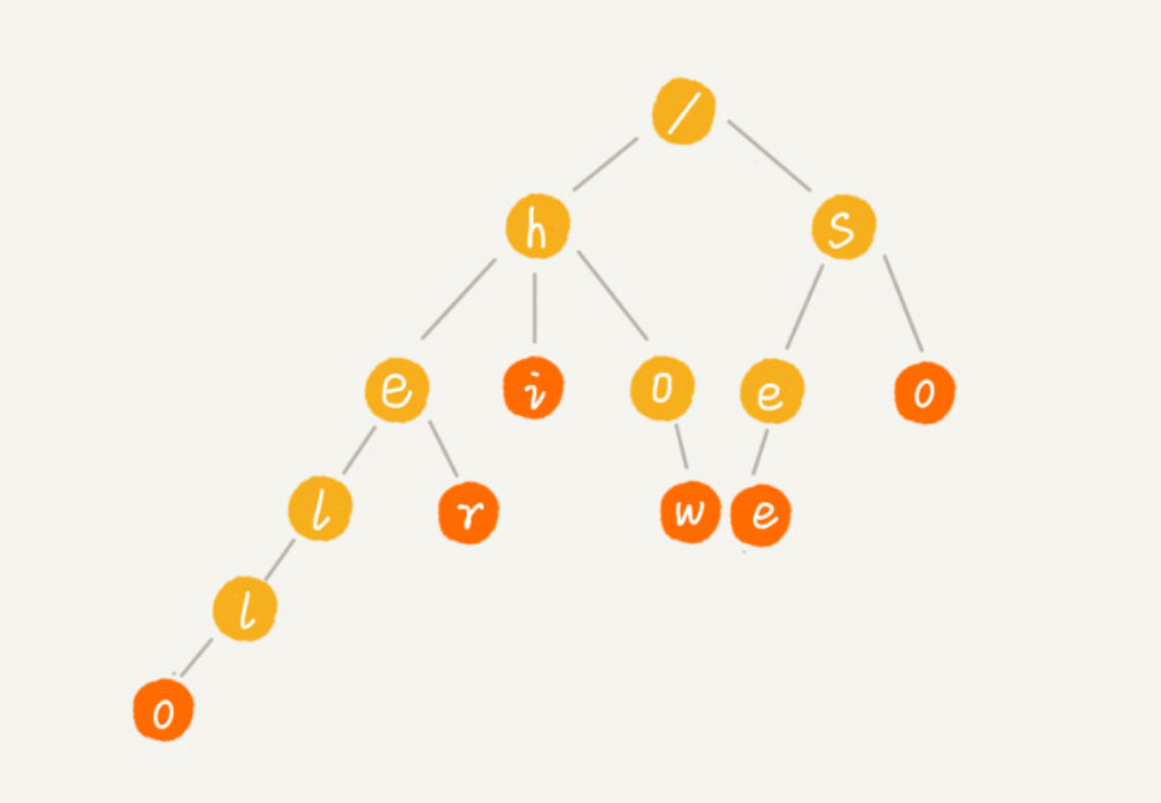
Trie 树占用内存太多。 Trie 树不适合精确匹配查找,这种问题更适合用散列表或者红黑树来解决。Trie 树比较适合的是查找前缀匹配的字符串。
AC自动机 Aho-Corasick算法
场景:敏感词过滤。 AC 自动机实际上就是在 Trie 树之上,加了类似 KMP 的 next 数组,只不过此处的 next 数组是构建在树上罢了。
查找
二分查找
时间复杂度是O(logn),42亿个数中使用二分查找一个数据,最多需要比较32次。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = (low + high) / 2;
if (a[mid] == value) {
return mid;
} else if (a[mid] < value) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return -1;
}
注意的点:
- 循环退出条件 low<=high,不是low<high
- mid的取值 mid=(low+high)/2是有问题的。如果low和high比较大,两者和就可能溢出。改进方法:mid=low+(high-low)/2,也就是mid=low+((high-low)»1)。
- low和high的更新 如果是low=mid或high=mid,可能发生死循环。比如,low=high=3,但是3这个位置不是查找的数据。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 二分查找的递归实现
public int bsearch(int[] a, int n, int val) {
return bsearchInternally(a, 0, n - 1, val);
}
private int bsearchInternally(int[] a, int low, int high, int value) {
if (low > high) return -1;
int mid = low + ((high - low) >> 1);
if (a[mid] == value) {
return mid;
} else if (a[mid] < value) {
return bsearchInternally(a, mid+1, high, value);
} else {
return bsearchInternally(a, low, mid-1, value);
}
}
二分查找适用的场合:
- 保存在数组中
- 有序数据
- 数据量不能太大。因为数组需要连续的内存空间。
- 更适合静态数据,没有频繁的数据插入、删除操作,这样可以做一次排序O(nlogn),然后使用二分O(logn)进行多次查找。对于有频繁数据插入、删除的操作,使用二叉树更好。
散列表和二叉树支持动态数据的查找,但是需要消耗数据以外的额外内存空间。二叉树底层依赖数组,最省内存空间。 二分查找在查找某一值附近的边界值时,比散列表和二叉树更有优势。比如查找最后一个小于等于给定值的元素。
二分查找算法的变体
- 查找第一个等于给定元素的值
- 查找最后一个等于给定元素的值
- 查找第一个大于等于给定元素的值
- 查找第一个小于等于给定元素的值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 查找第一个等于给定元素的值
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if ((mid == 0) || (a[mid - 1] != value)) return mid;
else high = mid - 1;
}
}
return -1;
}
跳表 Skip List
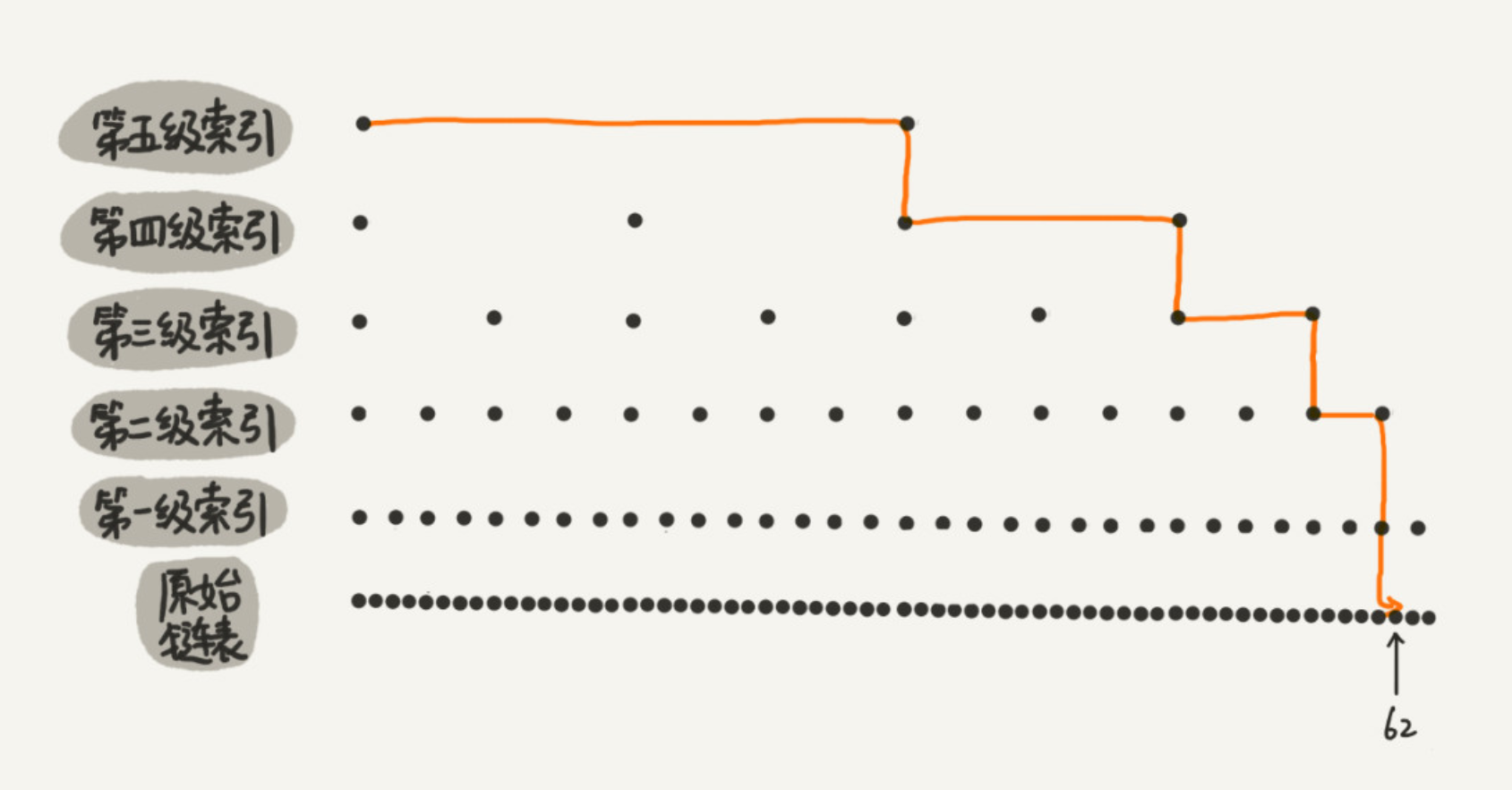
为一个值有序的链表建立多级索引,比如每2个节点提取一个节点到上一级,我们把抽出来的那一级叫做索引或索引层。像这种为链表建立多级索引的数据结构就称为跳表。
Redis使用跳表来实现有序集合。
跳表使用空间换时间的设计思路,通过构建多级索引来提高查询的效率,实现了基于链表的“二分查找”。跳表是一种动态数据结构,支持快速的插入、删除、查找操作,每两个节点抽出一个做为上级节点时,时间复杂度都是 O(logn)。跳表的空间复杂度是 O(n)。跳表支持动态的插入、删除操作,而且插入、删除操作的时间复杂度也是 O(logn)。
当我们不停地往跳表中插入数据时,如果我们不更新索引,就有可能出现某 2 个索引结点之间数据非常多的情况。极端情况下,跳表还会退化成单链表。解决方法:当我们往跳表中插入数据的时候,我们可以选择同时将这个数据插入到部分索引层中。通过一个随机函数,来决定将这个结点插入到哪几级索引中,比如随机函数生成了值 K,那我们就将这个结点添加到第一级到第 K 级这 K 级索引中。
跳表的实现非常灵活,可以通过改变索引构建策略,有效平衡执行效率和内存消耗。实现起来比红黑树更简单。
散列表 Hash table
散列表用的是数组支持按照下标随机访问数据的特性,所以散列表其实就是数组的一种扩展,由数组演化而来。可以说,如果没有数组,就没有散列表。查询平均是O(1)。
散列冲突:
再好的散列函数也无法避免散列冲突。那究竟该如何解决散列冲突问题呢?我们常用的散列冲突解决方法有两类,开放寻址法(open addressing)和链表法(chaining)。 Java 中 LinkedHashMap 就采用了链表法解决冲突,ThreadLocalMap 是通过线性探测的开放寻址法来解决冲突。
开放寻址法
当我们往散列表中插入数据时,如果某个数据经过散列函数散列之后,存储位置已经被占用了,我们就从当前位置开始,依次往后查找,看是否有空闲位置,直到找到为止。
当数据量比较小、装载因子小的时候,适合采用开放寻址法。这也是 Java 中的ThreadLocalMap使用开放寻址法解决散列冲突的原因。
开放寻址法的散列表储存在数组中,比起链表来说,冲突的代价更高,更浪费内存。但这种方式序列化起来比较简单。
装载因子只能小于1,当接近1时,就会有大量的散列冲突,导致再散列,性能会下降很多。
链表法
在散列表中,每个“桶(bucket)”或者“槽(slot)”会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。
基于链表的散列冲突处理方法比较适合存储大对象、大数据量的散列表,而且,比起开放寻址法,它更加灵活,支持更多的优化策略,比如用红黑树代替链表。Java 中的 LinkedHashMap 就采用了链表法解决冲突。最差的查找时间是O(logn)。
散列表的装载因子 load factor
1
散列表的装载因子=填入表中的元素个数/散列表的长度
装载因子越大,说明空闲位置越少,冲突越多,散列表的性能会下降。
当散列表的装载因子超过某个阈值时,就需要进行扩容。装载因子阈值需要选择得当。如果太大,会导致冲突过多;如果太小,会导致内存浪费严重。装载因子阈值的设置要权衡时间、空间复杂度。如果内存空间不紧张,对执行效率要求很高,可以降低负载因子的阈值;相反,如果内存空间紧张,对执行效率要求又不高,可以增加负载因子的值,甚至可以大于 1。
扩容方案
如果一次就完成扩容,需要一次性将原有散列表的数据重新计算哈希值,会很耗时。
所以扩容可以分批完成,当装载因子触达阈值之后,我们只申请新空间,但并不将老的数据搬移到新散列表中。当有新数据要插入时,我们将新数据插入新散列表中,并且从老的散列表中拿出一个数据放入到新散列表。每次插入一个数据到散列表,我们都重复上面的过程。对于查询操作,为了兼容了新、老散列表中的数据,我们先从新散列表中查找,如果没有找到,再去老的散列表中查找。
这种实现方式,任何情况下,插入一个数据的时间复杂度都是 O(1)。
应用
在 JDK1.8 版本中,为了对 HashMap 做进一步优化,我们引入了红黑树。而当链表长度太长(默认超过 8)时,链表就转换为红黑树。我们可以利用红黑树快速增删改查的特点,提高 HashMap 的性能。当红黑树结点个数少于 8 个的时候,又会将红黑树转化为链表。因为在数据量较小的情况下,红黑树要维护平衡,比起链表来,性能上的优势并不明显。
LRU:如果只是一个单链表,那么时间复杂度是O(n)。但是可以通过散列表和双向链表结合,来达到O(1)的时间复杂度。散列表用O(1)可以找到需要的数据,双向链表可以使数据的增删也变成O(1)。
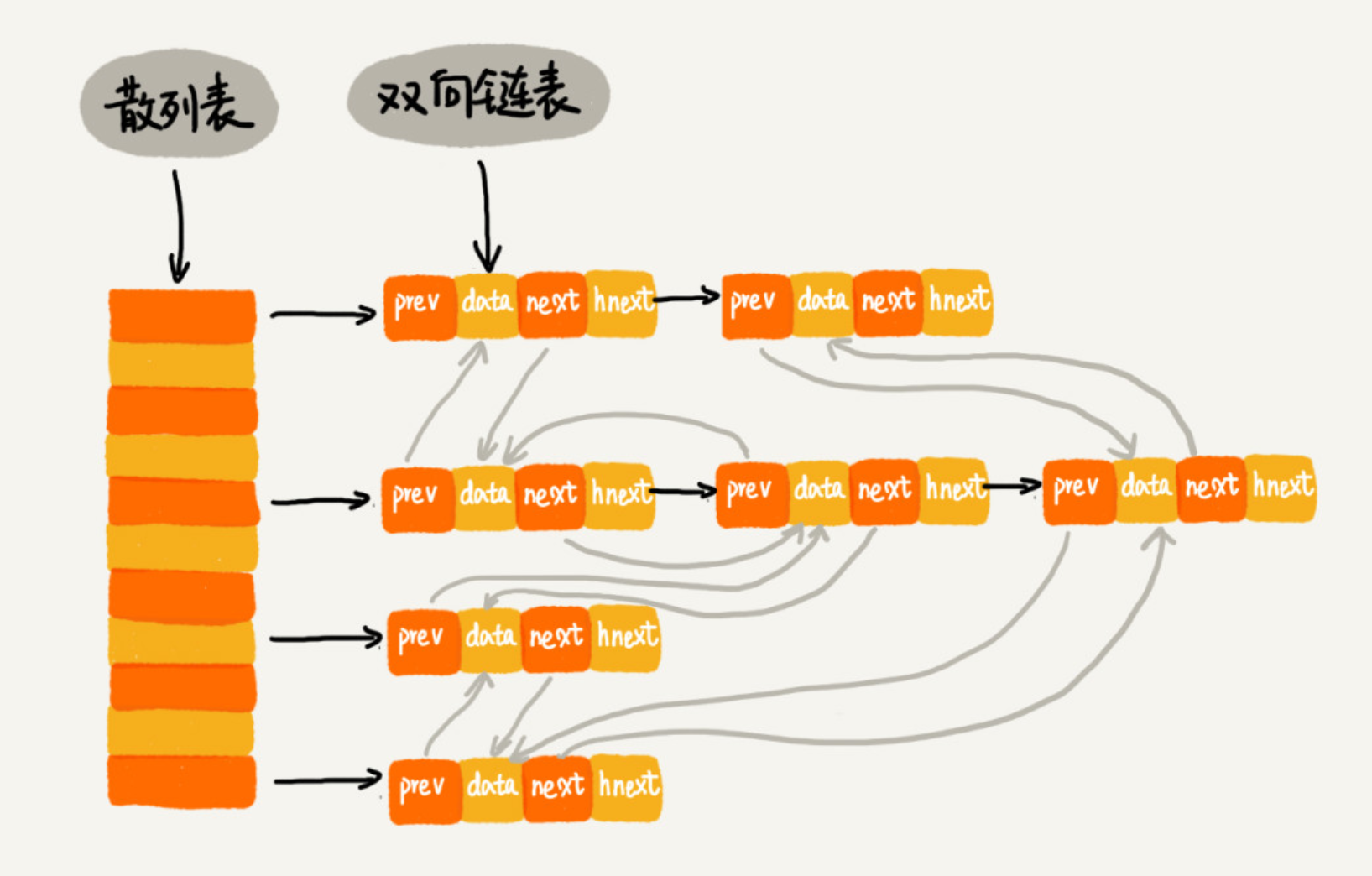
Java的 LinkedHashMap 就采用上面LRU的实现算法,这里的Linked并不是说用链表解决散列冲突,而是用链表实现了数据插入和访问的顺序,新put和新get的数据都在链表尾。
Redis有序集合 Redis有序集合里面有key(键值)和score(分值)。按key将数据构建成一个散列表,按score构建跳表,来保证用key检索或用score区间检索的高效。
位运算
基础知识
& 与, 或, ^ 非 - 左移 «。左边的将被丢弃,右边补0。
- 右移 »。两种情况:
- 无符号数,左侧补0
- 右符号数,左侧补0或者1,根据最左侧的位来决定
技巧
一个整数减去1,再和原数做与运算,会把改整数最后边的一个1变成0。
计算一个整数的二进制有多少个1
检查下面代码中的错误
int GetOneCount(int n)
{
int count = 0;
int bit = 1;
for (int i = 0; i < sizeof(int)*8; i++)
{
if (bit&n > 0)
count++;
bit = bit << 1;
}
return count;
}
上面第一次写出来,错误的地方有:
- &的优先级比>低,所以应该是 (bit&n)>0
- bit是int的,有符号,如果n是负数,与运算后首位是1,还是负数,不能用>0来判断
改正后:
int GetOneCount(int n)
{
int count = 0;
unsigned int flag = 1;
while(flag)
{
if (n&flag)
count++;
flag = flag << 1;
}
return count;
}
优化的做法,有几个1循环几次:
int GetOneCount(int n)
{
int count = 0;
while(n)
{
count++;
n = (n-1)&n;
}
return count;
}
测试需要覆盖到:
- 正数(包括1,0x7FFFFFFF)
- 负数(包括0x80000000,0xFFFFFFFF)
- 0
布隆过滤器 Bloom Filter
本质上布隆过滤器是一种数据结构,比较巧妙的概率型数据结构(probabilistic data structure),特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”。
相比于传统的 List、Set、Map 等数据结构,它更高效、占用空间更少,但是缺点是其返回的结果是概率性的,而不是确切的。
原始的位图:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class BitMap { // Java中char类型占16bit,也即是2个字节
private char[] bytes;
private int nbits;
public BitMap(int nbits) {
this.nbits = nbits;
this.bytes = new char[nbits/16+1];
}
public void set(int k) {
if (k > nbits) return;
int byteIndex = k / 16;
int bitIndex = k % 16;
bytes[byteIndex] |= (1 << bitIndex);
}
public boolean get(int k) {
if (k > nbits) return false;
int byteIndex = k / 16;
int bitIndex = k % 16;
return (bytes[byteIndex] & (1 << bitIndex)) != 0;
}
}
如果用位图,数据的范围很大的时候就不方便。比如数据个数是 1 千万,数据的范围是 1 到 10 亿,用位图就需要能储存10亿的位图。
布隆过滤器的做法是,我们使用一个 1 亿个二进制大小的位图,然后通过哈希函数,对数字进行处理,让它落在这 1 到 1 亿范围内。比如我们把哈希函数设计成 f(x)=x%n。其中,x 表示数字,n 表示位图的大小(1 亿),也就是,对数字跟位图的大小进行取模求余。这样会产生冲突,为了减少冲突,就用多个不同的hash函数,同时用多个位来确定一个数。
布隆过滤器非常适合这种不需要 100% 准确的、允许存在小概率误判的大规模判重场景。 Java 中的 BitSet 类就是一个位图,Redis 也提供了 BitMap 位图类,Google 的 Guava 工具包提供了 BloomFilter 布隆过滤器的实现。
二叉树
分类
Linked list就是特殊化的Tree,Tree就是特殊化的Graph。
- binary tree. 二叉树
- binary search tree. (alias: ordered binary tree, sorted binary tree) 空树,或满足下面的特点:左子树上所有节点的值都小于它的根节点的值,右子树上所有节点的值都大于它的根节点的值,Recursively,左右子树也分别为二叉查找树。
- 红黑树是一种特殊的二叉搜索树,最坏情况下的O效率更高
定义
- 高度 Height, 深度 Depth,层 Level
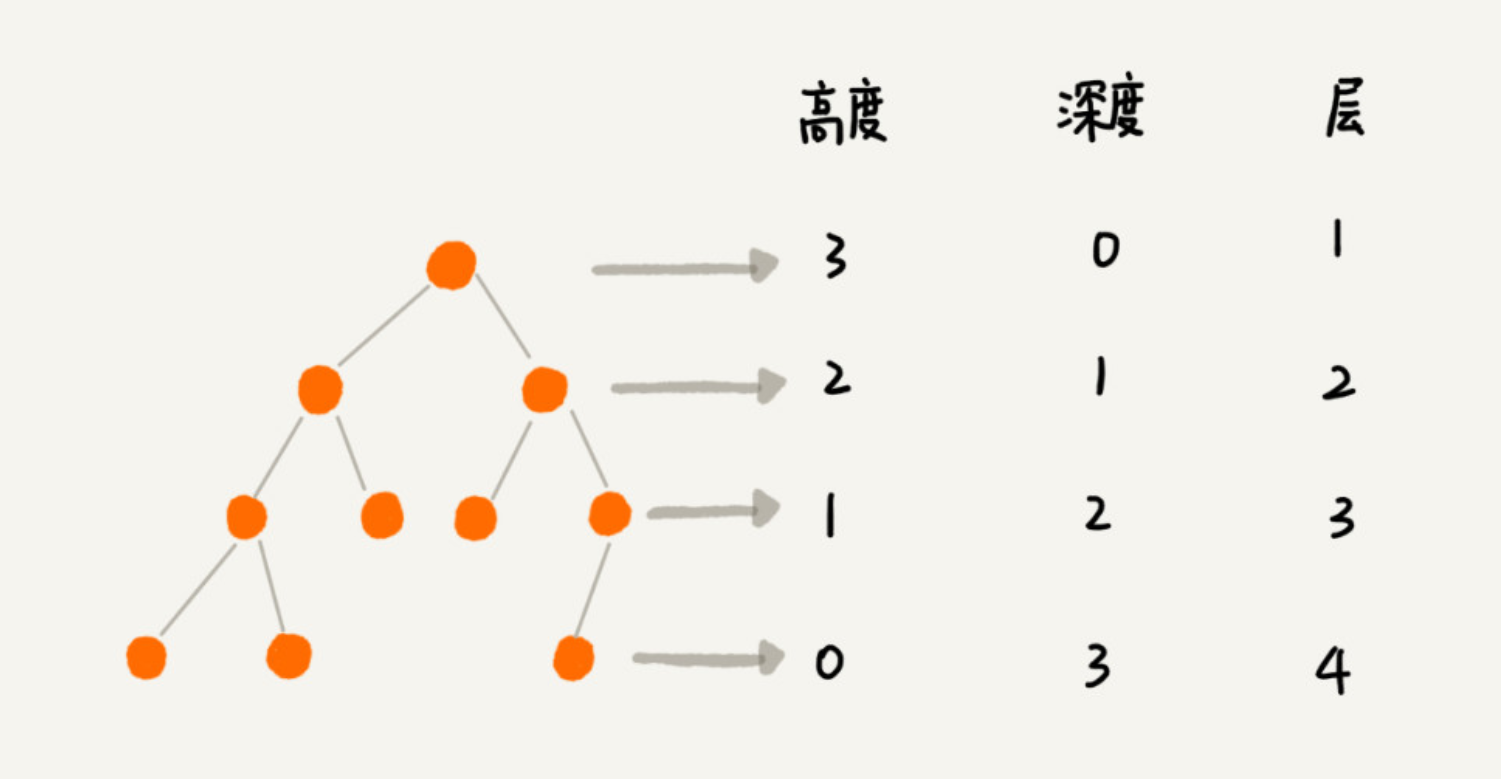
- 编号 2 的二叉树中,叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点,这种二叉树就叫作满二叉树。
- 编号 3 的二叉树中,叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大,这种二叉树叫作完全二叉树。
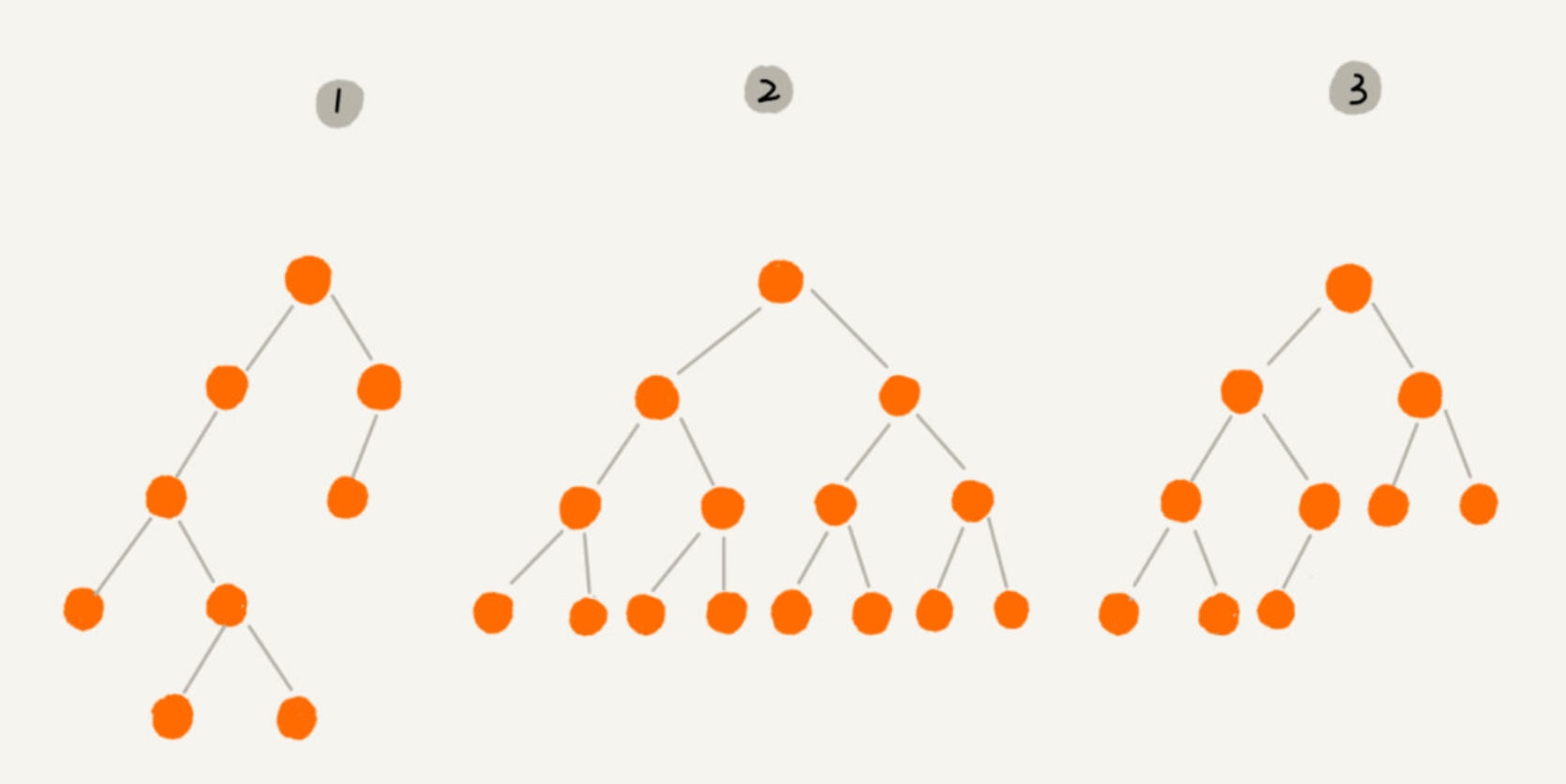
链式存储 和 顺序存储
链式存储:比较常见,每个节点还有左右两个指针,分别指向左子节点和右子节点。 顺序存储:基于数组。如果节点 X 存储在数组中下标为 i 的位置,下标为 2 * i 的位置存储的就是左子节点,下标为 2 * i + 1 的位置存储的就是右子节点。反过来,下标为 i/2 的位置存储就是它的父节点。但是如果是非完全二叉树,就会浪费存储空间。
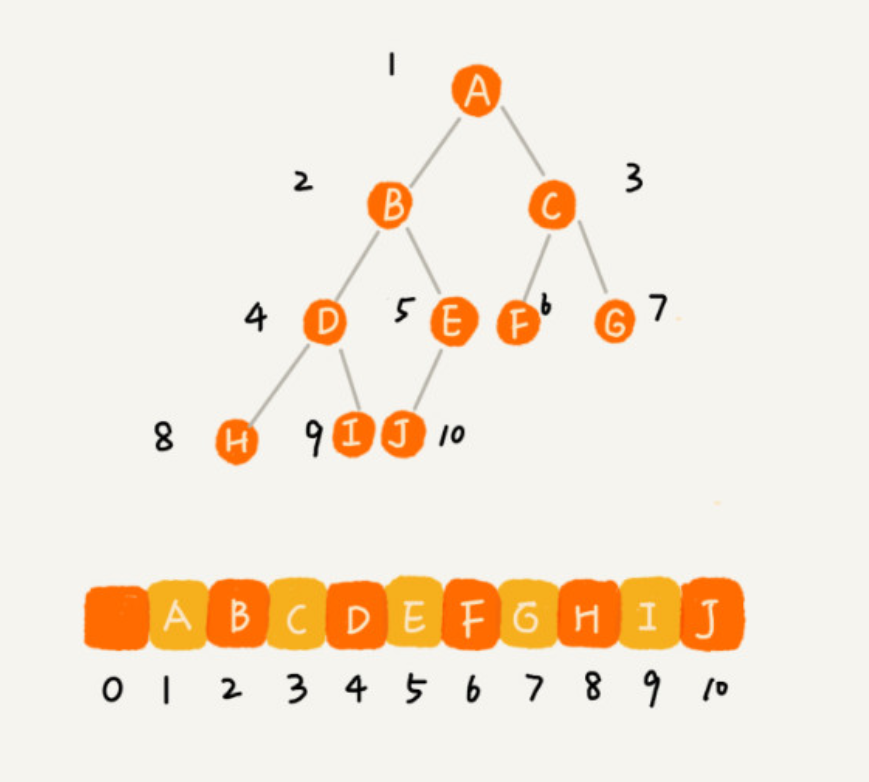
二叉搜索树
- 查找一个节点 我们先取根节点,如果它等于我们要查找的数据,那就返回。如果要查找的数据比根节点的值小,那就在左子树中递归查找;如果要查找的数据比根节点的值大,那就在右子树中递归查找。
- 添加一个节点 二叉查找树的插入过程有点类似查找操作。新插入的数据一般都是在叶子节点上,所以我们只需要从根节点开始,依次比较要插入的数据和节点的大小关系。如果要插入的数据比节点的数据大,并且节点的右子树为空,就将新数据直接插到右子节点的位置;如果不为空,就再递归遍历右子树,查找插入位置。同理,如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;如果不为空,就再递归遍历左子树,查找插入位置。
- 删除一个节点 二叉查找树的查找、插入操作都比较简单易懂,但是它的删除操作就比较复杂了 。针对要删除节点的子节点个数的不同,我们需要分三种情况来处理。 第一种情况是,如果要删除的节点没有子节点,我们只需要直接将父节点中,指向要删除节点的指针置为 null。比如图中的删除节点 55。 第二种情况是,如果要删除的节点只有一个子节点(只有左子节点或者右子节点),我们只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的子节点就可以了。比如图中的删除节点 13。 第三种情况是,如果要删除的节点有两个子节点,这就比较复杂了。我们需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上。然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以,我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 18。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public void delete(int data) {
Node p = tree; // p指向要删除的节点,初始化指向根节点
Node pp = null; // pp记录的是p的父节点
while (p != null && p.data != data) {
pp = p;
if (data > p.data) p = p.right;
else p = p.left;
}
if (p == null) return; // 没有找到
// 要删除的节点有两个子节点
if (p.left != null && p.right != null) { // 查找右子树中最小节点
Node minP = p.right;
Node minPP = p; // minPP表示minP的父节点
while (minP.left != null) {
minPP = minP;
minP = minP.left;
}
p.data = minP.data; // 将minP的数据替换到p中
p = minP; // 下面就变成了删除minP了
pp = minPP;
}
// 删除节点是叶子节点或者仅有一个子节点
Node child; // p的子节点
if (p.left != null) child = p.left;
else if (p.right != null) child = p.right;
else child = null;
if (pp == null) tree = child; // 删除的是根节点
else if (pp.left == p) pp.left = child;
else pp.right = child;
}
红黑树(平衡二叉搜索树) Red-Black Tree
红黑树的起源:前面的二叉查找树是最常用的一种二叉树,它支持快速插入、删除、查找操作,各个操作的时间复杂度跟树的高度成正比,理想情况下,时间复杂度是 O(logn)。不过,二叉查找树在频繁的动态更新过程中,可能会出现树的高度远大于 log2n 的情况,从而导致各个操作的效率下降。极端情况下,二叉树会退化为链表,时间复杂度会退化到 O(n)。所以有了平衡二叉查找树。
定义:红黑树中的节点,一类被标记为黑色,一类被标记为红色。除此之外,一棵红黑树还需要满足这样几个要求:
- 根节点是黑色的;
- 每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据;
- 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;

验证二叉搜索树
中序把树遍历出来,然后去重、排序后进行比较。
1
2
3
4
5
6
7
8
9
# 代码看起来简单,但是list(sorted(set()))效率很低
def isValidBST(self, root):
inorder = self.inorder(root)
return inorder == list(sorted(set(inorder)))
def inorder(self, root):
if root is None:
return []
return self.inorder(root.left) + [root.val] + self.inorder(root.right)
改进,效率更高:
1
2
3
4
5
6
7
8
9
10
11
12
13
def isValidBST(self, root):
self.prev = None
return self.helper(root)
def helper(self, root):
if root is None:
return True
if not self.helper(root.left):
return False
if self.prev and self.prev.val >= root.val:
return False
self.prev = root
return self.helper(root.right)
一种简单的遍历,每个节点都应该在一个值的范围内
1
2
3
4
5
6
7
8
def isValidBST(root, min, max):
if root is not None:
return True
if min != None && root.val <= min:
return False
if max != None && root.val >= max:
return False
return isValidBST(root.left, min, root.val) && isValidBST(root.right, root.val, max)
二叉树的最小公共祖先
给出两个节点,找到他们的最小公共祖先。
遍历。分别遍历左右子树,如果一边找到另外一边没找到,就返回找到的一边。如果两边都找到,就说明当前节点就是最小公共祖先。
1
TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q)
1
2
3
4
5
6
TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
return left == null ? right : right == null ? left : root;
}
如果是二叉搜索树,则可以更简单。
递归。如果当前节点>p和q,那么就往右搜索。反之,往左搜索。
1
2
3
4
5
6
def lowestCommonAncestor(root, p, q):
if root.val > p.val && root.val > q.val:
return lowestCommonAncestor(root.left, p, q)
if root.val < p.val && root.val < q.val:
return lowestCommonAncestor(root.right, p, q)
return root
不用递归。
1
2
3
4
5
6
7
8
def lowestCommonAncestor(root, p, q):
while root:
if root.val > p.val && root.val > q.val:
root = root.left
elif root.val < p.val && root.val < q.val:
root = root.right
else:
return root
三种遍历
按根所处的位置来分:(时间复杂度是O(n))
- Pre-order 前序遍历(根,左,右)
- In-order 中序遍历(左,根,右)
- Post-order 后序遍历(左,右,根)
如果是普通的二叉树,这三种方式遍历的意义不大。如果是二叉搜索树,中序遍历出来是一个有序数组。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def preorder(root):
if root:
traverse_path.append(root.val)
preorder(root.left)
preorder(root.right)
def inorder(root):
if root:
inorder(root.left)
traverse_path.append(root.val)
inorder(root.right)
def postorder(root):
if root:
postorder(root.left)
postorder(root.right)
traverse_path.append(root.val)
散列表 vs 二叉树
二叉树退化成链表的时候,查找的时间复杂度就退化成了O(n)。 平衡二叉查找树的时间复杂度和树的高度成正比,是O(height),也就是小于O(logn)。
散列表的添加、删除、查找可以做到O(1)。
但散列表也有劣势:
- 散列表中的数据是无序存储的,如果要输出有序的数据,需要先进行排序。而对于二叉查找树来说,我们只需要中序遍历,就可以在 O(n) 的时间复杂度内,输出有序的数据序列。
- 散列表扩容耗时很多,而且当遇到散列冲突时,性能不稳定,尽管二叉查找树的性能不稳定,但是在工程中,我们最常用的平衡二叉查找树的性能非常稳定,时间复杂度稳定在 O(logn)。
- 尽管散列表的查找等操作的时间复杂度是常量级的,但因为哈希冲突的存在,这个常量不一定比 logn 小,所以实际的查找速度可能不一定比 O(logn) 快。加上哈希函数的耗时,也不一定就比平衡二叉查找树的效率高。
- 散列表的构造比二叉查找树要复杂,需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡二叉查找树只需要考虑平衡性这一个问题,而且这个问题的解决方案比较成熟、固定。
- 为了避免过多的散列冲突,散列表装载因子不能太大,特别是基于开放寻址法解决冲突的散列表,不然会浪费一定的存储空间。
AVL vs 红黑树
AVL 树是一种高度平衡的二叉树,所以查找的效率非常高,但是,有利就有弊,AVL 树为了维持这种高度的平衡,就要付出更多的代价。每次插入、删除都要做调整,就比较复杂、耗时。所以,对于有频繁的插入、删除操作的数据集合,使用 AVL 树的代价就有点高了。红黑树只是做到了近似平衡,并不是严格的平衡,所以在维护平衡的成本上,要比 AVL 树要低。所以,红黑树的插入、删除、查找各种操作性能都比较稳定。对于工程应用来说,要面对各种异常情况,为了支撑这种工业级的应用,我们更倾向于这种性能稳定的平衡二叉查找树。
红黑树是一种平衡二叉查找树。它是为了解决普通二叉查找树在数据更新的过程中,复杂度退化的问题而产生的。红黑树的高度近似 log2n,所以它是近似平衡,插入、删除、查找操作的时间复杂度都是 O(logn)。
B+树
B+树的特点:
- 每个节点中子节点的个数不能超过 m,也不能小于 m/2;
- 根节点的子节点个数可以不超过 m/2,这是一个例外;
- m 叉树只存储索引,并不真正存储数据,这个有点儿类似跳表;
- 通过链表将叶子节点串联在一起,这样可以方便按区间查找;
- 一般情况,根节点会被存储在内存中,其他节点存储在磁盘中。
B-树(B树)的特点:
- B+ 树中的节点不存储数据,只是索引,而 B 树中的节点存储数据;
- B 树中的叶子节点并不需要链表来串联。
算法思想
贪心算法 Greedy Algorithm
例子:背包问题,最短路径,零钱问题。 贪心算法不一定是最优解。
分治 Divide and Conquer
分而治之 ,也就是将原问题划分成 n 个规模较小,并且结构与原问题相似的子问题,递归地解决这些子问题,然后再合并其结果,就得到原问题的解。
分治算法的递归实现中,每一层递归都会涉及这样三个操作:
- 分解:将原问题分解成一系列子问题;
- 解决:递归地求解各个子问题,若子问题足够小,则直接求解;
- 合并:将子问题的结果合并成原问题。
分治算法能解决的问题,一般需要满足下面这几个条件:
- 原问题与分解成的小问题具有相同的模式;
- 原问题分解成的子问题可以独立求解,子问题之间没有相关性,这一点是分治算法跟动态规划的明显区别;
- 具有分解终止条件,也就是说,当问题足够小时,可以直接求解;
- 可以将子问题合并成原问题,而这个合并操作的复杂度不能太高,否则就起不到减小算法总体复杂度的效果了。
回溯算法
回溯算法的思想非常简单,大部分情况下,都是用来解决广义的搜索问题,也就是,从一组可能的解中,选择出一个满足要求的解。回溯算法非常适合用递归来实现,在实现的过程中,剪枝操作是提高回溯效率的一种技巧。利用剪枝,我们并不需要穷举搜索所有的情况,从而提高搜索效率。
尽管回溯算法的原理非常简单,但是却可以解决很多问题,比如深度优先搜索、八皇后、0-1 背包问题、图的着色、旅行商问题、数独、全排列、正则表达式匹配等等。
进入回溯先检查退出条件,再看是否进入下一个回溯。
八皇后:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int[] result = new int[8];//全局或成员变量,下标表示行,值表示queen存储在哪一列
public void cal8queens(int row) { // 调用方式:cal8queens(0);
if (row == 8) { // 8个棋子都放置好了,打印结果
printQueens(result);
return; // 8行棋子都放好了,已经没法再往下递归了,所以就return
}
for (int column = 0; column < 8; ++column) { // 每一行都有8中放法
if (isOk(row, column)) { // 有些放法不满足要求
result[row] = column; // 第row行的棋子放到了column列
cal8queens(row+1); // 考察下一行
}
}
}
private boolean isOk(int row, int column) {//判断row行column列放置是否合适
int leftup = column - 1, rightup = column + 1;
for (int i = row-1; i >= 0; --i) { // 逐行往上考察每一行
if (result[i] == column) return false; // 第i行的column列有棋子吗?
if (leftup >= 0) { // 考察左上对角线:第i行leftup列有棋子吗?
if (result[i] == leftup) return false;
}
if (rightup < 8) { // 考察右上对角线:第i行rightup列有棋子吗?
if (result[i] == rightup) return false;
}
--leftup; ++rightup;
}
return true;
}
private void printQueens(int[] result) { // 打印出一个二维矩阵
for (int row = 0; row < 8; ++row) {
for (int column = 0; column < 8; ++column) {
if (result[row] == column) System.out.print("Q ");
else System.out.print("* ");
}
System.out.println();
}
System.out.println();
}
动态规划 Dynamic Programming
模型:多阶段决策最优解模型。三个特征:
- 最优子结构,问题的最优解包含子问题的最优解。
- 无后效性,第一层含义是,在推导后面阶段的状态的时候,我们只关心前面阶段的状态值,不关心这个状态是怎么一步一步推导出来的。第二层含义是,某阶段状态一旦确定,就不受之后阶段的决策影响。
- 重复子问题,不同的决策序列,到达某个相同的阶段时,可能会产生重复的状态。
大部分动态规划能解决的问题,都可以通过回溯算法来解决,只不过回溯算法解决起来效率比较低,时间复杂度是指数级的。动态规划算法,在执行效率方面,要高很多。尽管执行效率提高了,但是动态规划的空间复杂度也提高了,所以,动态规划是一种空间换时间的算法思想。
0-1背包问题
有一个最多能装重量是w的背包,有多种重量的物品items,问w背包中装items最多能装的重量是多少?
创建一个一维数组,每个物品都有放和不放两种情况,把每个物品放和不放,所占用的重量都列出来,然后就知道背包能装的最多东西的重量是多少了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int knapsack2(int[] items, int n, int w) {
boolean[] states = new boolean[w+1]; // 默认值false
states[0] = true; // 第一行的数据要特殊处理,可以利用哨兵优化
if (items[0] <= w) {
states[items[0]] = true;
}
for (int i = 1; i < n; ++i) { // 动态规划
for (int j = w-items[i]; j >= 0; --j) {//把第i个物品放入背包
if (states[j]==true) states[j+items[i]] = true;
}
}
for (int i = w; i >= 0; --i) { // 输出结果
if (states[i] == true) return i;
}
return 0;
}
升级版本: 刚才只涉及背包重量和物品重量,我们现在引入物品价值这一变量。对于一组不同重量、不同价值、不可分割的物品,我们选择将某些物品装入背包,在满足背包最大重量限制的前提下,背包中可装入物品的总价值最大是多少呢?
用回溯算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private int maxV = Integer.MIN_VALUE; // 结果放到maxV中
private int[] items = {2,2,4,6,3}; // 物品的重量
private int[] value = {3,4,8,9,6}; // 物品的价值
private int n = 5; // 物品个数
private int w = 9; // 背包承受的最大重量
public void finditems(int i, int cw, int cv) { // 调用f(0, 0, 0)
if (cw == w || i == n) { // cw==w表示装满了,i==n表示物品都考察完了
if (cv > maxV) maxV = cv;
return;
}
finditems(i+1, cw, cv); // 选择不装第i个物品
if (cw + weight[i] <= w) {
finditems(i+1,cw+weight[i], cv+value[i]); // 选择装第i个物品
}
}
动态规划:
还是把整个求解过程分为 n 个阶段,每个阶段会决策一个物品是否放到背包中。每个阶段决策完之后,背包中的物品的总重量以及总价值,会有多种情况,也就是会达到多种不同的状态。 用一个二维数组 states[n][w+1],来记录每层可以达到的不同状态。不过这里数组存储的值不再是 boolean 类型的了,而是当前状态对应的最大总价值。我们把每一层中 (i, cw) 重复的状态(节点)合并,只记录 cv 值最大的那个状态,然后基于这些状态来推导下一层的状态。
时间复杂度是 O(n x w),空间复杂度也是 O(n x w)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public static int knapsack3(int[] weight, int[] value, int n, int w) {
int[][] states = new int[n][w+1];
for (int i = 0; i < n; ++i) { // 初始化states
for (int j = 0; j < w+1; ++j) {
states[i][j] = -1;
}
}
states[0][0] = 0;
if (weight[0] <= w) {
states[0][weight[0]] = value[0];
}
for (int i = 1; i < n; ++i) { //动态规划,状态转移
for (int j = 0; j <= w; ++j) { // 不选择第i个物品
if (states[i-1][j] >= 0) states[i][j] = states[i-1][j];
}
for (int j = 0; j <= w-weight[i]; ++j) { // 选择第i个物品
if (states[i-1][j] >= 0) {
int v = states[i-1][j] + value[i];
if (v > states[i][j+weight[i]]) {
states[i][j+weight[i]] = v;
}
}
}
}
// 找出最大值
int maxvalue = -1;
for (int j = 0; j <= w; ++j) {
if (states[n-1][j] > maxvalue) maxvalue = states[n-1][j];
}
return maxvalue;
}
两种动态规划的解题思路
假设我们有一个 n 乘以 n 的矩阵 w[n][n]。矩阵存储的都是正整数。棋子起始位置在左上角,终止位置在右下角。我们将棋子从左上角移动到右下角。每次只能向右或者向下移动一位。从左上角到右下角,会有很多不同的路径可以走。我们把每条路径经过的数字加起来看作路径的长度。那从左上角移动到右下角的最短路径长度是多少呢?
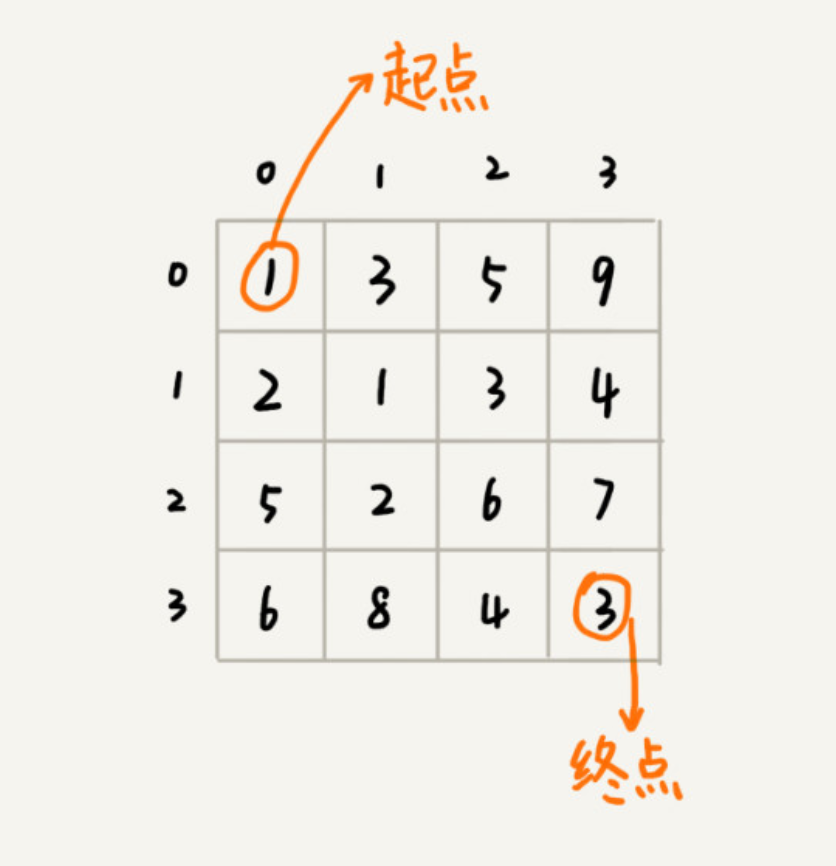
用回溯的方法实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private int minDist = Integer.MAX_VALUE; // 全局变量或者成员变量
// 调用方式:minDistBacktracing(0, 0, 0, w, n);
public void minDistBT(int i, int j, int dist, int[][] w, int n) {
// 到达了n-1, n-1这个位置了,这里看着有点奇怪哈,你自己举个例子看下
if (i == n && j == n) {
if (dist < minDist) minDist = dist;
return;
}
if (i < n) { // 往下走,更新i=i+1, j=j
minDistBT(i + 1, j, dist+w[i][j], w, n);
}
if (j < n) { // 往右走,更新i=i, j=j+1
minDistBT(i, j+1, dist+w[i][j], w, n);
}
}
状态转移表法
先画出一个状态表。状态表一般都是二维的,所以你可以把它想象成二维数组。其中,每个状态包含三个变量,行、列、数组值。我们根据决策的先后过程,从前往后,根据递推关系,分阶段填充状态表中的每个状态。最后,我们将这个递推填表的过程,翻译成代码,就是动态规划代码了。
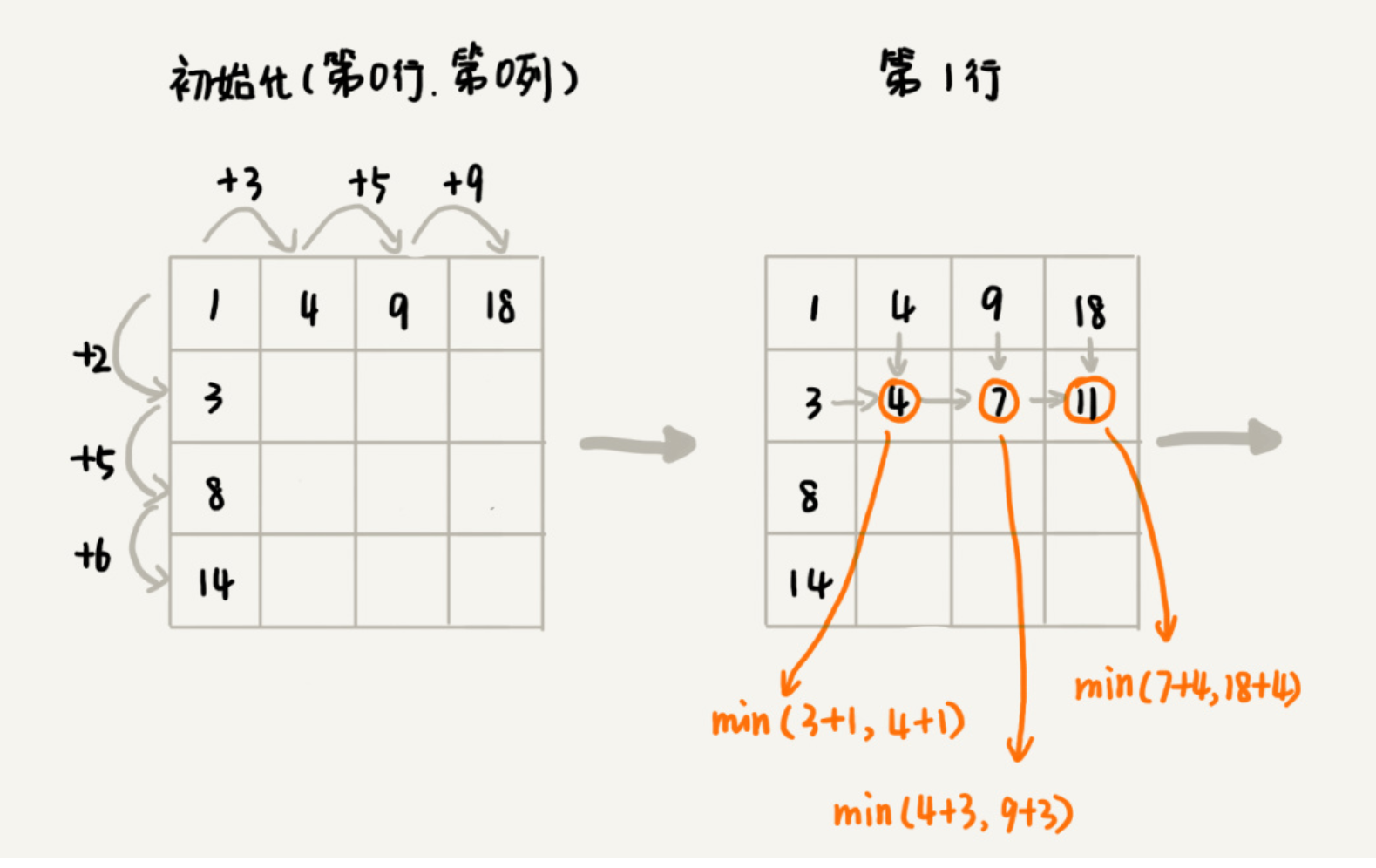
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int minDistDP(int[][] matrix, int n) {
int[][] states = new int[n][n];
int sum = 0;
for (int j = 0; j < n; ++j) { // 初始化states的第一行数据
sum += matrix[0][j];
states[0][j] = sum;
}
sum = 0;
for (int i = 0; i < n; ++i) { // 初始化states的第一列数据
sum += matrix[i][0];
states[i][0] = sum;
}
for (int i = 1; i < n; ++i) {
for (int j = 1; j < n; ++j) {
states[i][j] =
matrix[i][j] + Math.min(states[i][j-1], states[i-1][j]);
}
}
return states[n-1][n-1];
}
状态转移方程法:有点类似递归的解题思路。我们需要分析,某个问题如何通过子问题来递归求解,也就是所谓的最优子结构。根据最优子结构,写出递归公式,也就是所谓的状态转移方程。有了状态转移方程,代码实现就非常简单了。一般情况下,我们有两种代码实现方法,一种是递归加“备忘录”,另一种是迭代递推。
状态转移方程
1
min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
private int[][] matrix = { {1,3,5,9}, {2,1,3,4},{5,2,6,7},{6,8,4,3} };
private int n = 4;
private int[][] mem = new int[4][4];
public int minDist(int i, int j) {
// 调用minDist(n-1, n-1);
if (i == 0 && j == 0) return matrix[0][0];
if (mem[i][j] > 0) return mem[i][j];
int minLeft = Integer.MAX_VALUE;
if (j-1 >= 0) {
minLeft = minDist(i, j-1);
}
int minUp = Integer.MAX_VALUE;
if (i-1 >= 0) {
minUp = minDist(i-1, j);
}
int currMinDist = matrix[i][j] + Math.min(minLeft, minUp);
mem[i][j] = currMinDist;
return currMinDist;
}
递归 Recursion
递归的特点
- 一个问题的解可以分解为几个子问题的解
- 这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样
- 存在递归终止条件,即必须有一个明确的递归结束条件,称之为递归出口
问题:警惕堆栈溢出。
求解思路
最关键的是: 写出递推公式,找到终止条件。 写递归代码就是找到如何将大问题分解为小问题的规律,并且基于此写出递推公式,然后再推敲终止条件,最后将递推公式和终止条件翻译成代码。
例子:有n个台阶,每次可以上1个或者2个台阶,有多少种走法? 分析:到第n个台阶的走法数,其实是到n-1个台阶的走法数(再上一个台阶)+n-2个台阶的走法数(再上两个台阶) 所以递推公式就是:f(n)=f(n-1)+f(n-2) 终止条件是:f(1)=1, f(2)=2
1
2
3
4
5
int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
return f(n-1) + f(n-2);
}
如果一个问题 A 可以分解为 B、C、D,你可以假设子问题B、C、D已经解决,在此基础上思考如何解决问题 A。而且,你只需要思考问题A和子问题B、C、D两层之间的关系即可,不需要一层层往下思考子问题和子子问题,子问题和子子问题之间的关系。屏蔽掉递归细节,理解起来就简单多了。
递归的问题以及改进
- 警惕堆栈溢出
函数递归调用可能导致堆栈溢出,可以用变量来保存递归深度,超过该深度就返回,避免溢出。
- 警惕重复计算
比如前面的例子中,f(5)需要计算f(4)和f(3),f(4)需要计算f(3)和f(2),其中 f(3) 被重复计算。
上面例子里的代码可改造为:
1
2
3
4
5
6
7
8
9
10
11
12
13
public int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
// hasSolvedList可以理解成一个Map,key是n,value是f(n)
if (hasSolvedList.containsKey(n)) {
return hasSolvedList.get(n);
}
int ret = f(n-1) + f(n-2);
hasSolvedList.put(n, ret);
return ret;
}
递归的框架
注意递归有时有重复计算的情况,效率会降低。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def recursion(level, param1, param2, ...):
# recursion terminator
if level > MAX_LEVEL:
print_result
return
# process logic in current level
process_data(level, data...)
# drill down
recursion(level+1, p1, ...)
# reverse the current level status if needed
reverse_state(level)
分治 Divide & Conquer
如果分解的各个子问题可以独立运算,那么就可以用分治的方法。分治通常也用递归来实现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def divide_conquer(problem, param1, param2, ...):
# recursion terminator
if problem is None:
print_result
return
# prepare data
data = prepare_data(problem)
subproblems = split_problem(problem, data)
# conquer subproblems
subresult1 = divide_conquer(subproblems[0], p1, ...)
subresult2 = divide_conquer(subproblems[1], p1, ...)
subresult3 = divide_conquer(subproblems[2], p1, ...)
...
# process and generate the final subresult
result = process_result(subresult1, subresult2, subresult3, ...)
计算x的n次方
采用分治的方法:从中间分开,两边乘,避免了重复运算。注意n是偶数和奇数的情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 递归的方法
def myPow(x, n):
if not n:
return 1
if n < 0:
return 1 / myPow(x, -n)
if n % 2:
return x * myPow(x, n-1)
return myPow(x*x, n/2)
# 非递归的方法
def myPow(x, n):
if n < 0:
x = 1/x
n = -n
pow = 1
while n:
if n & 1:
pow *= x
x *= x
n >>= 1
return pow
其它
拓扑排序
比如编译文件时,文件间的相互依赖关系。拓扑排序的结果并不是唯一的。拓扑排序里面不能出现环,所以是一个有向无环图。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class Graph {
private int v; // 顶点的个数
private LinkedList<Integer> adj[]; // 邻接表
public Graph(int v) {
this.v = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i) {
adj[i] = new LinkedList<>();
}
}
public void addEdge(int s, int t) { // s先于t,边s->t
adj[s].add(t);
}
}
- Kahn算法
Kahn 算法实际上用的是贪心算法思想。
定义数据结构的时候,如果 s 需要先于 t 执行,那就添加一条 s 指向 t 的边。所以,如果某个顶点入度为 0, 也就表示,没有任何顶点必须先于这个顶点执行,那么这个顶点就可以执行了。
我们先从图中,找出一个入度为 0 的顶点,将其输出到拓扑排序的结果序列中(对应代码中就是把它打印出来),并且把这个顶点从图中删除(也就是把这个顶点可达的顶点的入度都减 1)。我们循环执行上面的过程,直到所有的顶点都被输出。最后输出的序列,就是满足局部依赖关系的拓扑排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public void topoSortByKahn() {
int[] inDegree = new int[v]; // 统计每个顶点的入度
for (int i = 0; i < v; ++i) {
for (int j = 0; j < adj[i].size(); ++j) {
int w = adj[i].get(j); // i->w
inDegree[w]++;
}
}
LinkedList<Integer> queue = new LinkedList<>();
for (int i = 0; i < v; ++i) {
if (inDegree[i] == 0) queue.add(i);
}
while (!queue.isEmpty()) {
int i = queue.remove();
System.out.print("->" + i);
for (int j = 0; j < adj[i].size(); ++j) {
int k = adj[i].get(j);
inDegree[k]--;
if (inDegree[k] == 0) queue.add(k);
}
}
}
- DFS 算法
这个算法包含两个关键部分。 第一部分是通过邻接表构造逆邻接表。邻接表中,边 s->t 表示 s 先于 t 执行,也就是 t 要依赖 s。在逆邻接表中,边 s->t 表示 s 依赖于 t,s 后于 t 执行。为什么这么转化呢?这个跟我们这个算法的实现思想有关。 第二部分是这个算法的核心,也就是递归处理每个顶点。对于顶点 vertex 来说,我们先输出它可达的所有顶点,也就是说,先把它依赖的所有的顶点输出了,然后再输出自己。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public void topoSortByDFS() {
// 先构建逆邻接表,边s->t表示,s依赖于t,t先于s
LinkedList<Integer> inverseAdj[] = new LinkedList[v];
for (int i = 0; i < v; ++i) { // 申请空间
inverseAdj[i] = new LinkedList<>();
}
for (int i = 0; i < v; ++i) { // 通过邻接表生成逆邻接表
for (int j = 0; j < adj[i].size(); ++j) {
int w = adj[i].get(j); // i->w
inverseAdj[w].add(i); // w->i
}
}
boolean[] visited = new boolean[v];
for (int i = 0; i < v; ++i) { // 深度优先遍历图
if (visited[i] == false) {
visited[i] = true;
dfs(i, inverseAdj, visited);
}
}
}
private void dfs(
int vertex, LinkedList<Integer> inverseAdj[], boolean[] visited) {
for (int i = 0; i < inverseAdj[vertex].size(); ++i) {
int w = inverseAdj[vertex].get(i);
if (visited[w] == true) continue;
visited[w] = true;
dfs(w, inverseAdj, visited);
} // 先把vertex这个顶点可达的所有顶点都打印出来之后,再打印它自己
System.out.print("->" + vertex);
}
拓扑排序应用非常广泛,解决的问题的模型也非常一致。凡是需要通过局部顺序来推导全局顺序的,一般都能用拓扑排序来解决。除此之外,拓扑排序还能检测图中环的存在。对于 Kahn 算法来说,如果最后输出出来的顶点个数,少于图中顶点个数,图中还有入度不是 0 的顶点,那就说明,图中存在环。
最短路径(Dijkstra算法)
把每个岔路口看作一个顶点,岔路口与岔路口之间的路看作一条边,路的长度就是边的权重。如果路是单行道,我们就在两个顶点之间画一条有向边;如果路是双行道,我们就在两个顶点之间画两条方向不同的边。这样,整个地图就被抽象成一个有向有权图。
Dijkstra算法可以看作是动态规划,又有点像BFS,从起始点依次扩散出去,看周围各个顶点到起始点的最短距离。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
// 因为Java提供的优先级队列,没有暴露更新数据的接口,所以我们需要重新实现一个
private class PriorityQueue { // 根据vertex.dist构建小顶堆
private Vertex[] nodes;
private int count;
public PriorityQueue(int v) {
this.nodes = new Vertex[v+1];
this.count = v;
}
public Vertex poll() { // TODO: 留给读者实现... }
public void add(Vertex vertex) { // TODO: 留给读者实现...}
// 更新结点的值,并且从下往上堆化,重新符合堆的定义。时间复杂度O(logn)。
public void update(Vertex vertex) { // TODO: 留给读者实现...}
public boolean isEmpty() { // TODO: 留给读者实现...}
}
public void dijkstra(int s, int t) { // 从顶点s到顶点t的最短路径
int[] predecessor = new int[this.v]; // 用来还原最短路径
Vertex[] vertexes = new Vertex[this.v];
for (int i = 0; i < this.v; ++i) {
vertexes[i] = new Vertex(i, Integer.MAX_VALUE);
}
PriorityQueue queue = new PriorityQueue(this.v);// 小顶堆
boolean[] inqueue = new boolean[this.v]; // 标记是否进入过队列
vertexes[s].dist = 0;
queue.add(vertexes[s]);
inqueue[s] = true;
while (!queue.isEmpty()) {
Vertex minVertex= queue.poll(); // 取堆顶元素并删除
if (minVertex.id == t) break; // 最短路径产生了
for (int i = 0; i < adj[minVertex.id].size(); ++i) {
Edge e = adj[minVertex.id].get(i); // 取出一条minVetex相连的边
Vertex nextVertex = vertexes[e.tid]; // minVertex-->nextVertex
if (minVertex.dist + e.w < nextVertex.dist) { // 更新next的dist
nextVertex.dist = minVertex.dist + e.w;
predecessor[nextVertex.id] = minVertex.id;
if (inqueue[nextVertex.id] == true) {
queue.update(nextVertex); // 更新队列中的dist值
} else {
queue.add(nextVertex);
inqueue[nextVertex.id] = true;
}
}
}
}
// 输出最短路径
System.out.print(s);
print(s, t, predecessor);
}
private void print(int s, int t, int[] predecessor) {
if (s == t) return;
print(s, predecessor[t], predecessor);
System.out.print("->" + t);
}
我们用 vertexes 数组,记录从起始顶点到每个顶点的距离(dist)。起初,我们把所有顶点的 dist 都初始化为无穷大(也就是代码中的 Integer.MAX_VALUE)。我们把起始顶点的 dist 值初始化为 0,然后将其放到优先级队列中。
我们从优先级队列中取出 dist 最小的顶点 minVertex,然后考察这个顶点可达的所有顶点(代码中的 nextVertex)。如果 minVertex 的 dist 值加上 minVertex 与 nextVertex 之间边的权重 w 小于 nextVertex 当前的 dist 值,也就是说,存在另一条更短的路径,它经过 minVertex 到达 nextVertex。那我们就把 nextVertex 的 dist 更新为 minVertex 的 dist 值加上 w。然后,我们把 nextVertex 加入到优先级队列中。重复这个过程,直到找到终止顶点 t 或者队列为空。
以上就是 Dijkstra 算法的核心逻辑。除此之外,代码中还有两个额外的变量,predecessor 数组和 inqueue 数组。
predecessor 数组的作用是为了还原最短路径,它记录每个顶点的前驱顶点。最后,我们通过递归的方式,将这个路径打印出来。打印路径的 print 递归代码我就不详细讲了,这个跟我们在图的搜索中讲的打印路径方法一样。如果不理解的话,你可以回过头去看下那一节。
inqueue 数组是为了避免将一个顶点多次添加到优先级队列中。我们更新了某个顶点的 dist 值之后,如果这个顶点已经在优先级队列中了,就不要再将它重复添加进去了。
简易搜索引擎中使用的算法
搜索引擎大致可以分为四个部分:搜集、分析、索引、查询。
- 搜集:就是我们常说的利用爬虫爬取网页。
- 分析:主要负责网页内容抽取、分词,构建临时索引,计算 PageRank 值这几部分工作。
- 索引:主要负责通过分析阶段得到的临时索引,构建倒排索引。
- 查询:主要负责响应用户的请求,根据倒排索引获取相关网页,计算网页排名,返回查询结果给用户。
搜集
爬虫在爬取网页的过程中,涉及的四个重要的文件。其中,links.bin 和 bloom_filter.bin 这两个文件是爬虫自身所用的。另外的两个(doc_raw.bin、doc_id.bin)是作为搜集阶段的成果,供后面的分析、索引、查询用的。
待爬取网页链接文件:links.bin 在广度优先搜索爬取页面的过程中,爬虫会不停地解析页面链接,将其放到队列中。于是,队列中的链接就会越来越多,可能会多到内存放不下。所以,我们用一个存储在磁盘中的文件(links.bin)来作为广度优先搜索中的队列。爬虫从 links.bin 文件中,取出链接去爬取对应的页面。等爬取到网页之后,将解析出来的链接,直接存储到 links.bin 文件中。断点续传。
网页判重文件:bloom_filter.bin 使用布隆过滤器,我们就可以快速并且非常节省内存地实现网页的判重。
原始网页存储文件:doc_raw.bin 把多个网页存储在一个文件中。每个网页之间,通过一定的标识进行分隔,方便后续读取。 比如:doc1_id \t doc1_size \t doc1 \r\n\r\n
网页链接及其编号的对应文件:doc_id.bin 可以按照网页被爬取的先后顺序,从小到大依次编号。具体是这样做的:我们维护一个中心的计数器,每爬取到一个网页之后,就从计数器中拿一个号码,分配给这个网页,然后计数器加一。在存储网页的同时,我们将网页链接跟编号之间的对应关系,存储在另一个 doc_id.bin 文件中。
分析
抽取网页文本信息 依靠 HTML 标签来抽取网页中的文本信息。这个抽取的过程,大体可以分为两步。第一步是去掉 JavaScript 代码、CSS 格式以及下拉框中的内容。第二步是去掉所有 HTML 标签。 可以利用 AC 自动机这种多模式串匹配算法。
分词并创建临时索引:temp_index.bin 对于英文网页来说,分词只需要通过空格、标点符号等分隔符,将每个单词分割开来就可以了。对于中文来说,可以基于字典和规则的分词方法。 字典也叫词库,里面包含大量常用的词语。我们借助词库并采用最长匹配规则,来对文本进行分词。可以将词库中的单词,构建成Trie树。 每个网页的文本信息在分词完成之后,我们都得到一组单词列表。我们把单词与网页之间的对应关系,写入到一个临时索引文件中(tmp_Index.bin),这个临时索引文件用来构建倒排索引文件。 比如:term1_id \t doc_id \r\n
构建单词索引:term_id.bin 给每个单词编号,在temp_index.bin中使用单词id,而不是单词本身,来减小文件大小。使用散列表根据单词来查id。
索引
索引阶段主要负责将分析阶段产生的临时索引,构建成倒排索引。倒排索引( Inverted index)中记录了每个单词以及包含它的网页列表。
倒排索引文件(index.bin):term_id \t doc1_id,doc2_id,doc3_id,… \r\n
临时索引文件很大,无法一次性加载到内存中,搜索引擎一般会选择使用多路归并排序的方法来实现。
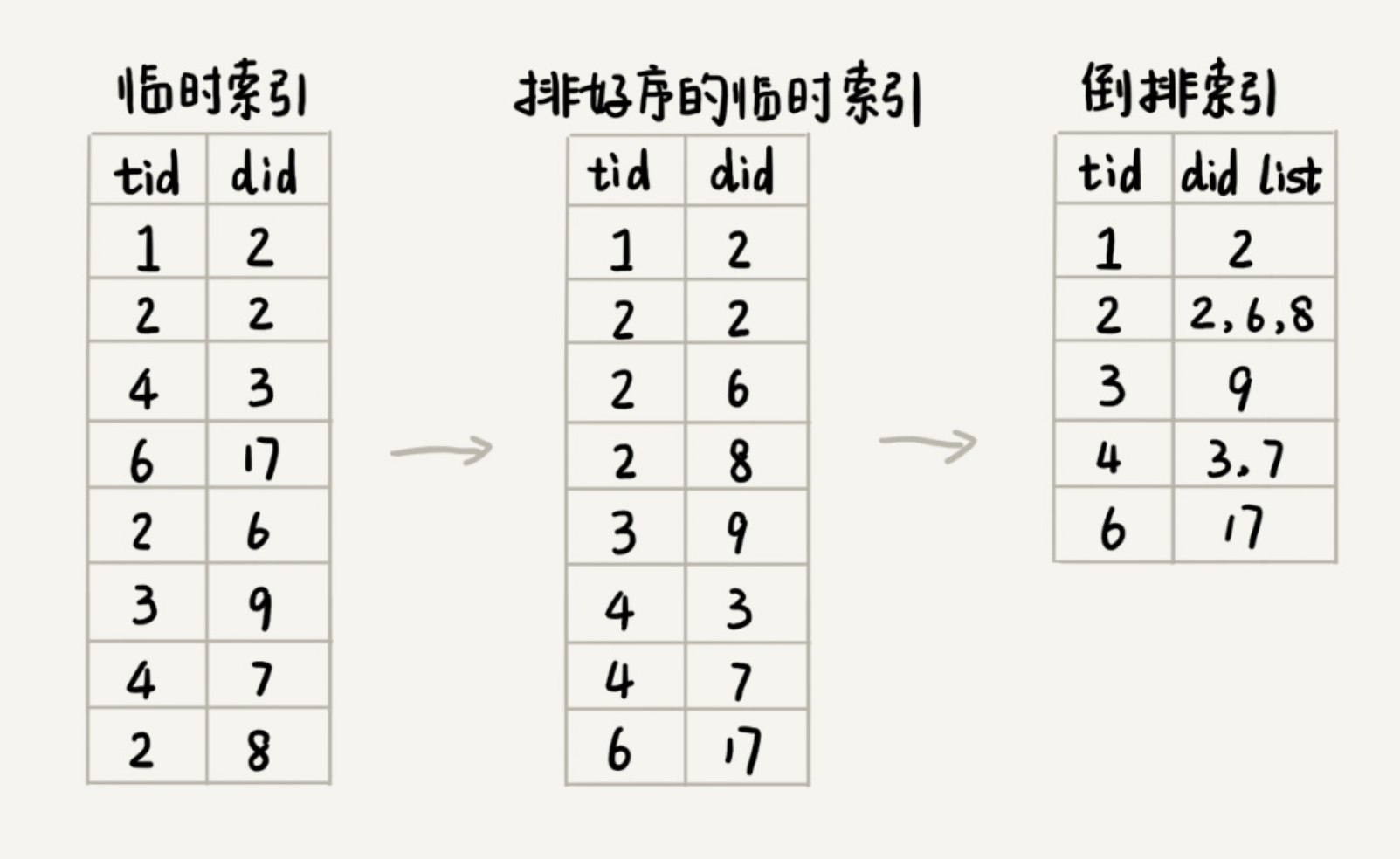
除了倒排文件之外,我们还需要一个文件(term_offset.bin),来记录每个单词编号在倒排索引文件中的偏移位置:tid1 \t offset1 \r\n
查询
前面几部准备好的文件有:
- doc_id.bin:记录网页链接和编号之间的对应关系
- term_id.bin:记录单词和编号之间的对应关系。
- index.bin:倒排索引文件,记录每个单词编号以及对应包含它的网页编号列表。
- term_offset.bin:记录每个单词编号在倒排索引文件中的偏移位置。
- 这四个文件中,除了倒排索引文件(index.bin)比较大之外,其他的都比较小。
k个单词 -> 找term id(term_id.bin) -> 找offset(term_offset.bin) -> 找网页列表(index.bin) -> 统计每个网页编号出现的次数,排序 -> 找网页连接(doc_id.bin)
练习
Leetcode 相关题目
- 链表
206,141,21,19,876
- 栈
20, 155, 232, 844, 224, 682, 496
思考题
假设我们有 10 万条 URL 访问日志,如何按照访问次数给 URL 排序? 遍历 10 万条数据,以 URL 为 key,访问次数为 value,存入散列表,同时记录下访问次数的最大值 K,时间复杂度 O(N)。如果 K 不是很大,可以使用桶排序,时间复杂度 O(N)。如果 K 非常大(比如大于 10 万),就使用快速排序,复杂度 O(NlogN)。
有两个字符串数组,每个数组大约有 10 万条字符串,如何快速找出两个数组中相同的字符串? 以第一个字符串数组构建散列表,key 为字符串,value 为出现次数。再遍历第二个字符串数组,以字符串为 key 在散列表中查找,如果 value 大于零,说明存在相同字符串。时间复杂度 O(N)。
散列表 vs 二叉搜索树。散列表的插入、删除、查找操作的时间复杂度可以做到常量级的 O(1),非常高效。而二叉查找树在比较平衡的情况下,插入、删除、查找操作时间复杂度才是 O(logn),相对散列表,好像并没有什么优势,那我们为什么还要用二叉查找树呢? 第一,散列表中的数据是无序存储的,如果要输出有序的数据,需要先进行排序。而对于二叉查找树来说,我们只需要中序遍历,就可以在 O(n) 的时间复杂度内,输出有序的数据序列。 第二,散列表扩容耗时很多,而且当遇到散列冲突时,性能不稳定,尽管二叉查找树的性能不稳定,但是在工程中,我们最常用的平衡二叉查找树的性能非常稳定,时间复杂度稳定在 O(logn)。 第三,笼统地来说,尽管散列表的查找等操作的时间复杂度是常量级的,但因为哈希冲突的存在,这个常量不一定比 logn 小,所以实际的查找速度可能不一定比 O(logn) 快。加上哈希函数的耗时,也不一定就比平衡二叉查找树的效率高。 第四,散列表的构造比二叉查找树要复杂,需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡二叉查找树只需要考虑平衡性这一个问题,而且这个问题的解决方案比较成熟、固定。 最后,为了避免过多的散列冲突,散列表装载因子不能太大,特别是基于开放寻址法解决冲突的散列表,不然会浪费一定的存储空间。 综合这几点,平衡二叉查找树在某些方面还是优于散列表的,所以,这两者的存在并不冲突。我们在实际的开发过程中,需要结合具体的需求来选择使用哪一个。
散列表 vs 跳表 vs 红黑树 散列表:插入删除查找都是O(1), 是最常用的,但其缺点是不能顺序遍历以及扩容缩容的性能损耗。适用于那些不需要顺序遍历,数据更新不那么频繁的。 跳表:插入删除查找都是O(logn), 并且能顺序遍历。缺点是空间复杂度O(n)。适用于不那么在意内存空间的,其顺序遍历和区间查找非常方便。 红黑树:插入删除查找都是O(logn), 中序遍历即是顺序遍历,稳定。缺点是难以实现,去查找不方便。其实跳表更佳,但红黑树已经用于很多地方了。
有一个包含 10 亿个搜索关键词的日志文件,如何快速获取到 Top 10 最热门的搜索关键词呢?可以使用的内存为 1GB. 可以选用散列表。顺序扫描这 10 亿个搜索关键词。当扫描到某个关键词时,我们去散列表中查询。如果存在,我们就将对应的次数加一;如果不存在,我们就将它插入到散列表,并记录次数为 1。以此类推,等遍历完这 10 亿个搜索关键词之后,散列表中就存储了不重复的搜索关键词以及出现的次数。然后,我们再根据前面讲的用堆求 Top K 的方法,建立一个大小为 10 的小顶堆,遍历散列表,依次取出每个搜索关键词及对应出现的次数,然后与堆顶的搜索关键词对比。如果出现次数比堆顶搜索关键词的次数多,那就删除堆顶的关键词,将这个出现次数更多的关键词加入到堆中。 假设 10 亿条搜索关键词中不重复的有 1 亿条,如果每个搜索关键词的平均长度是 50 个字节,那存储 1 亿个关键词起码需要 5GB 的内存空间,而散列表因为要避免频繁冲突,不会选择太大的装载因子,所以消耗的内存空间就更多了。而我们的机器只有 1GB 的可用内存空间,所以我们无法一次性将所有的搜索关键词加入到内存中。 可以根据哈希算法的这个特点,将 10 亿条搜索关键词先通过哈希算法分片到 10 个文件中。创建 10 个空文件 00,01,02,……,09。我们遍历这 10 亿个关键词,并且通过某个哈希算法对其求哈希值,然后哈希值同 10 取模,得到的结果就是这个搜索关键词应该被分到的文件编号。对这 10 亿个关键词分片之后,每个文件都只有 1 亿的关键词,去除掉重复的,可能就只有 1000 万个,每个关键词平均 50 个字节,所以总的大小就是 500MB。1GB 的内存完全可以放得下。针对每个包含 1 亿条搜索关键词的文件,利用散列表和堆,分别求出 Top 10,然后把这个 10 个 Top 10 放在一块,然后取这 100 个关键词中,出现次数最多的 10 个关键词,这就是这 10 亿数据中的 Top 10 最频繁的搜索关键词了。
合并一个逆序链表和一个正序链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
// 写了两个多小时,每行代码都值得注意!!! @_@
#include <iostream>
using namespace std;
struct ListNode{
int val;
struct ListNode* next;
ListNode(int v):val(v),next(NULL) {};
};
void printLN(struct ListNode *p)
{
int i = 0;
while(p)
{
if (i++ > 10)
return;
printf("%d->", p->val);
p = p->next;
}
printf("NULL\n");
return;
}
void rnm(struct ListNode **p1, struct ListNode **p2, struct ListNode **head, struct ListNode **tmp)
{
if (*p1 == NULL)
return;
rnm(&((*p1)->next), p2, head, tmp);
if (*head == NULL)
{
if (*p2 == NULL || (*p1)->val < (*p2)->val)
{
*head = *p1;
*tmp = *p1;
return;
}
else
{
*head = *p2;
*tmp = *p2;
*p2 = (*p2)->next;
}
}
while(*p2 != NULL && (*p1)->val > (*p2)->val)
{
(*tmp)->next = *p2;
*tmp = *p2;
*p2 = (*p2)->next;
}
(*tmp)->next = (*p1);
*tmp = *p1;
}
struct ListNode* merge(struct ListNode *p1, struct ListNode *p2)
{
if (p1 == NULL)
return p2;
struct ListNode *head = NULL;
struct ListNode *tmp = NULL;
rnm(&p1, &p2, &head, &tmp);
if (p2 == NULL)
tmp->next = NULL;
else
tmp->next = p2;
return head;
}
int main()
{
struct ListNode a1(66), a2(44), a3(22), a4(0);
struct ListNode b1(11), b2(33), b3(55), b4(77), b5(88);
a1.next = &a2;
a2.next = &a3;
a3.next = &a4;
b1.next = &b2;
b2.next = &b3;
b3.next = &b4;
b4.next = &b5;
struct ListNode *head = merge(&a2, &b4);
printLN(head);
return 0;
}
练习
Stack
[84] 柱状图中最大的矩形 [42] 接雨水 [739] 每日温度 [496] 下一个更大元素 [316] 去除重复字母 [901] 股票价格跨度 [402] 移掉K位数字 [581] 最短无序连续子数组
Comments powered by Disqus.